前言

前面两篇文章介绍了whited-style光线追踪模型，虽然可以得到不错的光照效果，但显然它依然不是物理准确的模型，原因如下：

  1. 光线亮度只是简单的数值，没有物理意义上的单位，而现实中光线的亮度是用特定的亮度单位表示的。
  2. 在计算着色时，使用了Blinn-Phong模型，而Blinn-Phong模型本身就是一个不准确的经验模型，使用这种模型的whited-style光线追踪当然也是不正确的
  3. whited-style光线追踪对于漫反射表面直接进行光照计算，并没有对漫反射的光线进行追踪。
  4. whited-style光线追踪对于反射表面进行镜面反射，难以模拟介于漫反射和镜面反射之间的光泽反射(Glossy Reflection)。

而基于辐射度量学、BRDF（双向反射分布函数）以及渲染方程的Physicallly-Based Rendering（简称PBR，基于物理的渲染）就可以完美解决这些问题，本文就简单介绍一下辐射度量学、BRDF以及渲染方程的基础概念。

 

辐射度量学

辐射度量学其实是对光照的一套测量系统和单位，它能够准确的描述光线的物理性质。

其中，需要明白几个关于光线的概念，分别为： 辐射能量(Radiant Energy)，辐射通量(Radiant Flux)，辐射强度(Radiant Intensity)，Irradiance，Radiance，接下来就对这些概念进行具体解释。

 

辐射能量(Radiant Energy)

辐射能量指的是辐射出来的电磁能量，记为Q，单位为J（焦耳）。可以用物理当中的做功的大小来进行类比。

 

辐射通量(Radiant Flux)

辐射通量也称为辐射功率(Radiant Power)，指的是辐射能量除以时间，也就是单位时间的能量，记为Φ，单位为W（瓦特）或者lm（流明）。同样也可以用物理当中的功率来进行类比。

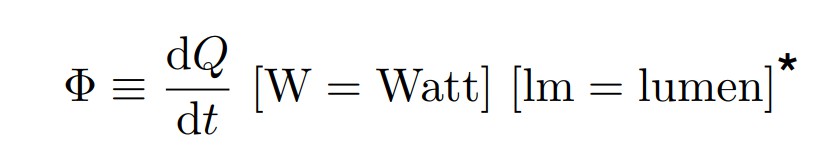
一般偏向用辐射通量来衡量物体的亮度，因为我们更关心的是单位时间的亮度效果，例如在购买白炽灯泡的时候是说30W亮度、50W亮度等，而在购买投影仪的时候则是说3000lm亮度、5000lm亮度等。

 

辐射强度(Radiant Intensity)

在具体的数学定义之前，先借助如下一张图建立对剩下3个概念的一些直观的理解

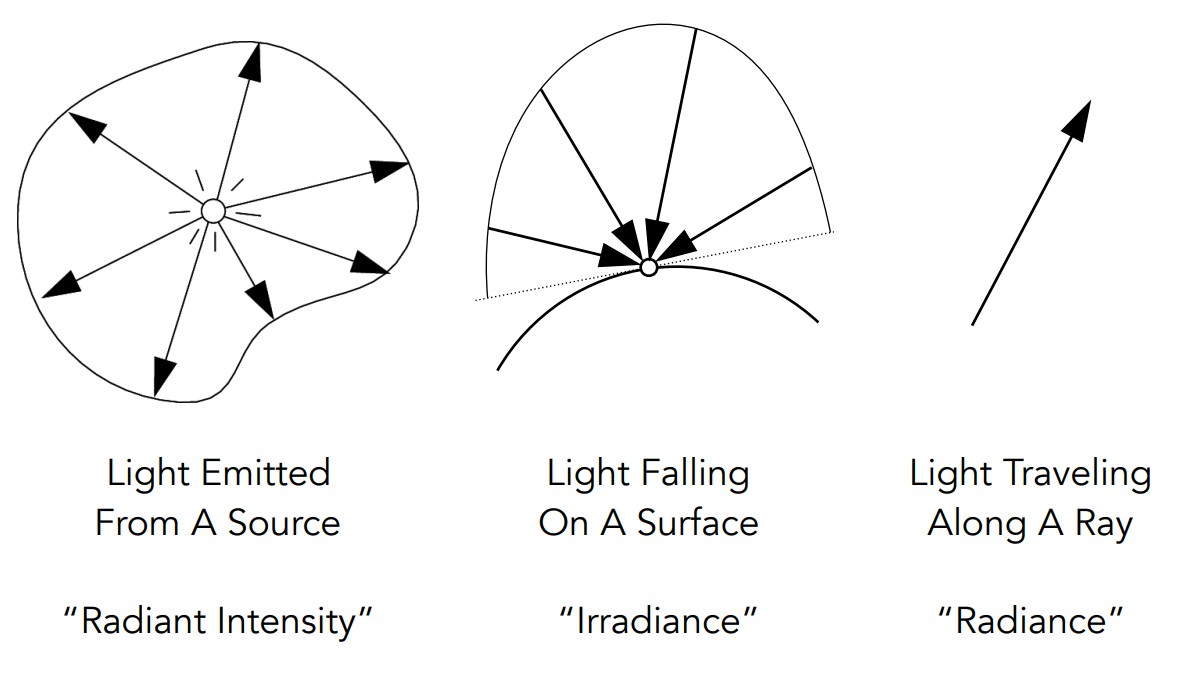
1 Radiant Intensity其实就是指从一个光源出发往某一方向上发射的光线的亮度，可以理解为某一方向上的辐射通量(Radiant Flux)

2 Irradiance指某一微小平面所接受到的光线亮度

3 Radiance指某一微小平面从某个方向接受（或者向某个方向发射）的光线的亮度

辐射强度一句话来说就是从光源发出的每单位立体角方向上的功率，单位为cd，关于辐射功率的定义在上文已经解释，这里唯一还不知道的就是立体角(Solid Angle)了。

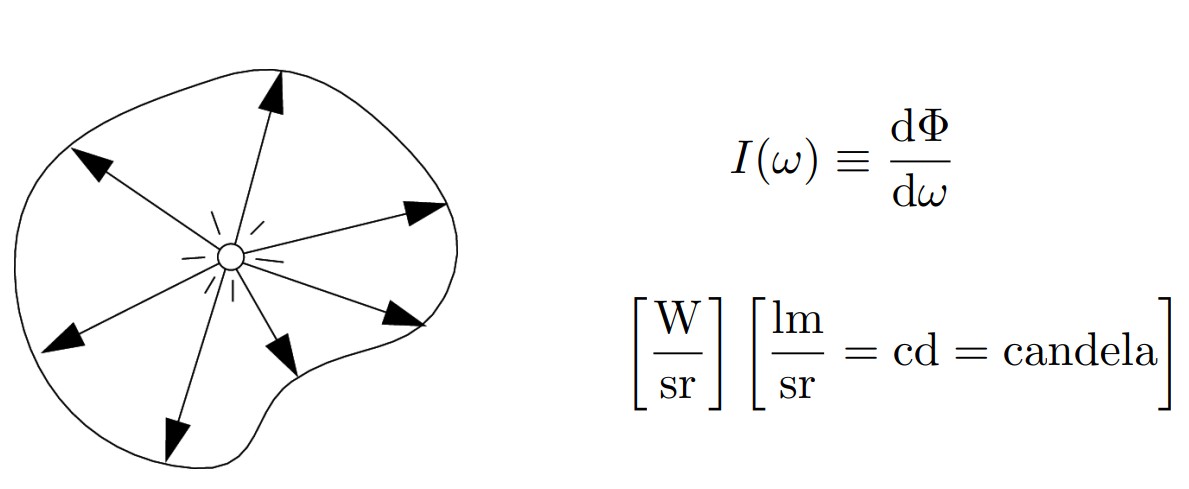
solid angle其实就是对应二维空间中圆的弧度在三维空间中球上的拓展。 首先在二维空间下计算弧度公式如下：

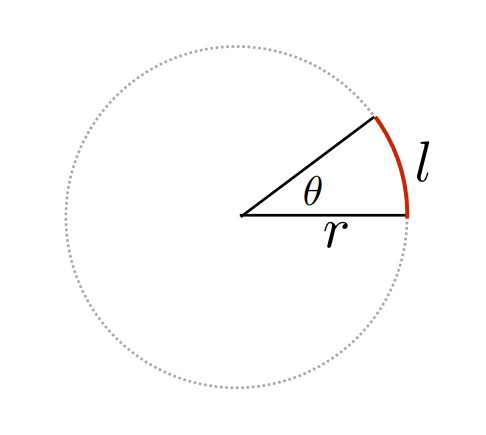
圆的弧度θ = l / r，即圆弧长度除以半径，整个圆形的弧度为2π，弧度的大小和扇形的角度有关，与圆形的大小没有直接关系。

那么对于三维的球体来说呢？

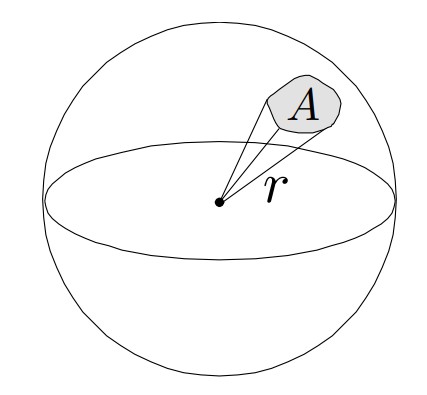
球体的立体角Ω 计算方式如下

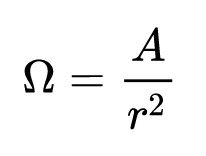
即立体角度所对应球上的投影面积除以半径的平方，整个球的立体角为4π，同样立体角和扇形体的两个角度有关，与球体大小没有直接关系。

那么对于辐射强度Radiant intensity的定义当中，微分立体角dw计算如下：

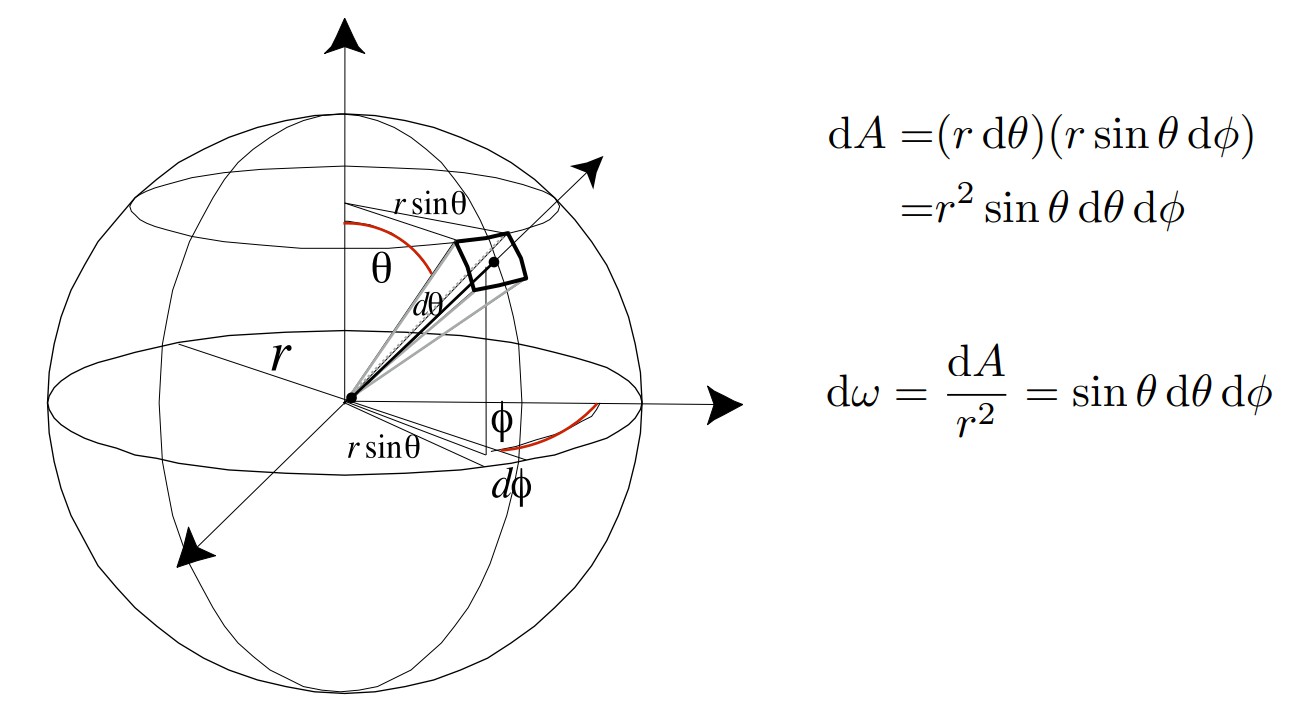
首先通过θ,Φ两个角度确定空间中一个方向，在这两个角度上分别增加一个微分值dθ和dΦ，则可以计算出如图中所示的球上的投影面积。其中rdθ就是微分面积元的高，rsinθdΦ是微分面积元的宽，二者相乘就是面积，再根据立体角的定义除以 r的平方 即可得到微分立体角了。

这里还可以验证下，对dw在整个球上积分：

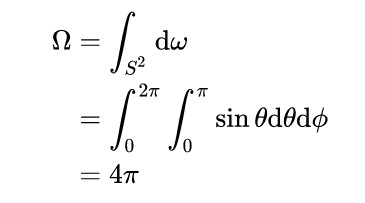
与之前所讲的球的立体角为4π一致。

注意在计算微分立体角之前，我们其实选定了空间当中的一个方向（由θ,Φ所确定），称这个方向为w，然后才在此基础之上分别对θ,Φ增加dθ,dΦ经计算得到最终的dw，因此辐射强度Radiant intensity的物理含义此时就很清楚了，为光源向某一方向的单位立体角发射出的光线的功率，简而言之就是光源在某个方向上的亮度！

对于各方向亮度一致的点光源计算Radiant Intensity如下

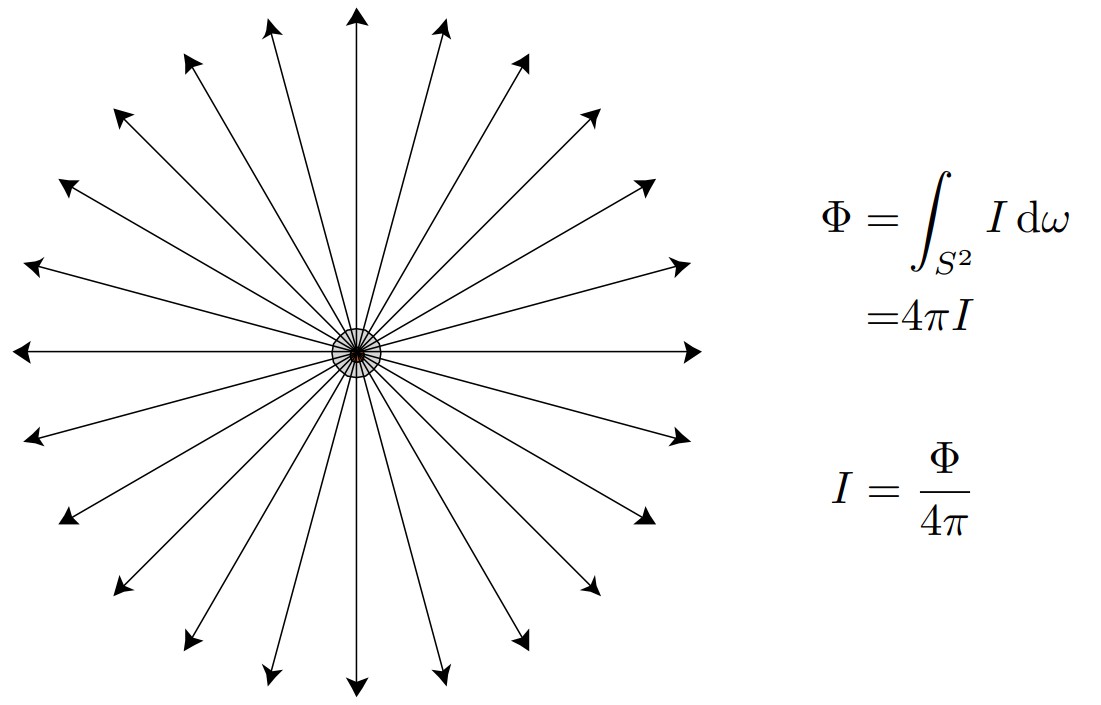
因为点光源所有方向上的亮度都与方向无关，因此立体角可以直接积分出来为4π，最终计算得点光源亮度I = Φ / 4π。 (如果不是各向同性光源的话这里的I(w)应该为一个关于w方向的的函数)。

 

Irradiance

Irradiance的定义是指每单位照射面积所接收到的辐射功率，单位为lux，如下图所示

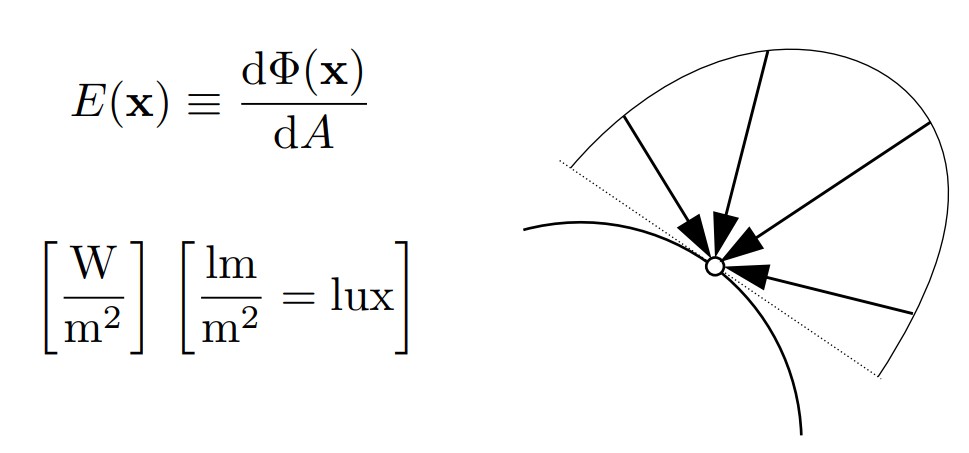
但上图中irradiance的定义是指光线与单位平面垂直时的计算方式，当光线与单位平面法线有一个夹角时，在计算时光线亮度需要乘上一个cosθ，如下图所示：

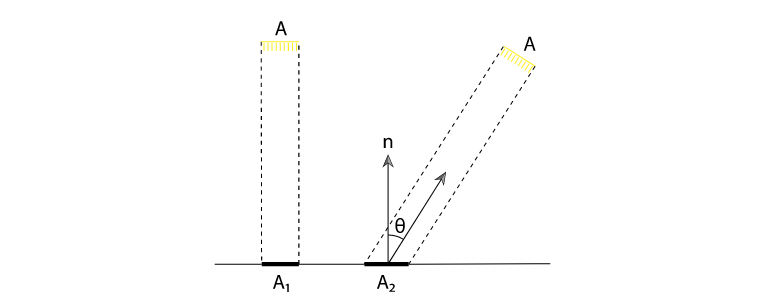
当光线垂直照射平面时，如上图左边所示，照射到平面上的面积与光线本身的“宽度一致”。但当光线斜着照射到平面时，此时的照射面积就不再是光线本身的“宽度”了，具体来说此时的照射面积A2 = A / cosθ。

反过来理解就是光线角度与平面法线有夹角时，相比于光线垂直照射平面，单位面积接受到的光线减少了

借助于irradiance，也可以很轻松的解释在Blinn-Phong所提到的Lambert’s Cosine Law为什么要乘以cosθ了。

对比现实中，一年四季的温度变化，就是因为太阳照射地球不同区域的光线角度不同。

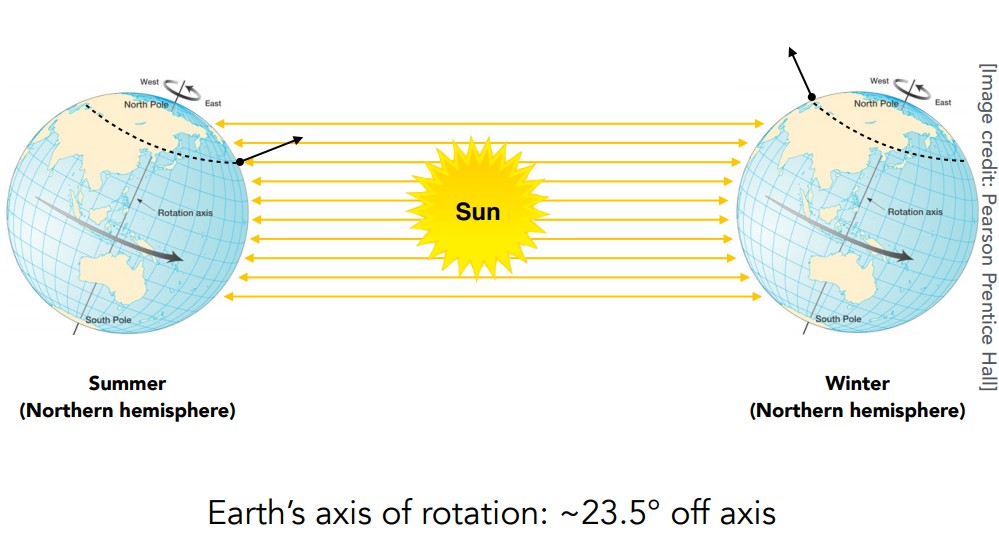
还有光线越远会更加衰减的现象也完全可以用irradiance解释，因为光的功率始终一致，离点光源越远所照射到的圆球面积也就越大，因此根据irradiance的式子，分母的单位面积值也就越大，irradiance也就衰减到越小（辐射强度Radiant Intensity不会衰减，因为只与立体角有关，与半径r无关），衰减速度为半径r的平方。

 

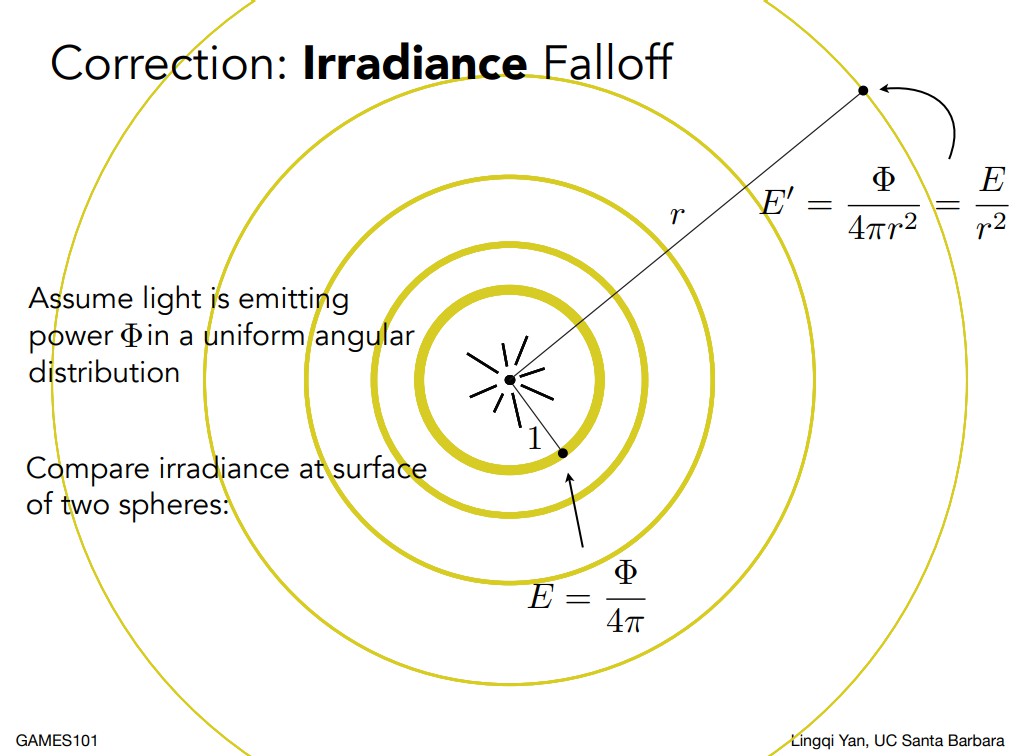
radiance

radiance一般用于衡量光线携带的能量，物理意义上是指每单位立体角，每单位垂直面积的功率，注意这里是两次微分，它同时指定了光的方向与照射到的表面所接受到的亮度。

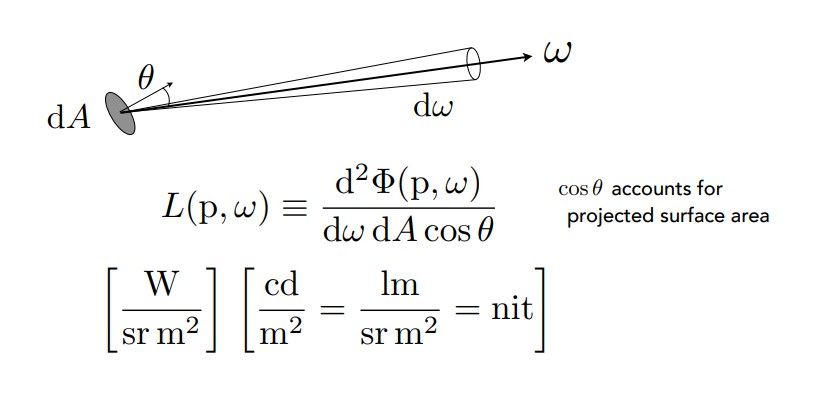
注意radiance既可以用于每单位垂直面积向每单位立体角发射（以及反射、折射等）的功率（Exiting Radiance），也可以用于每单位垂直面积从每单位立体角接收的功率（Incident Radiance）。

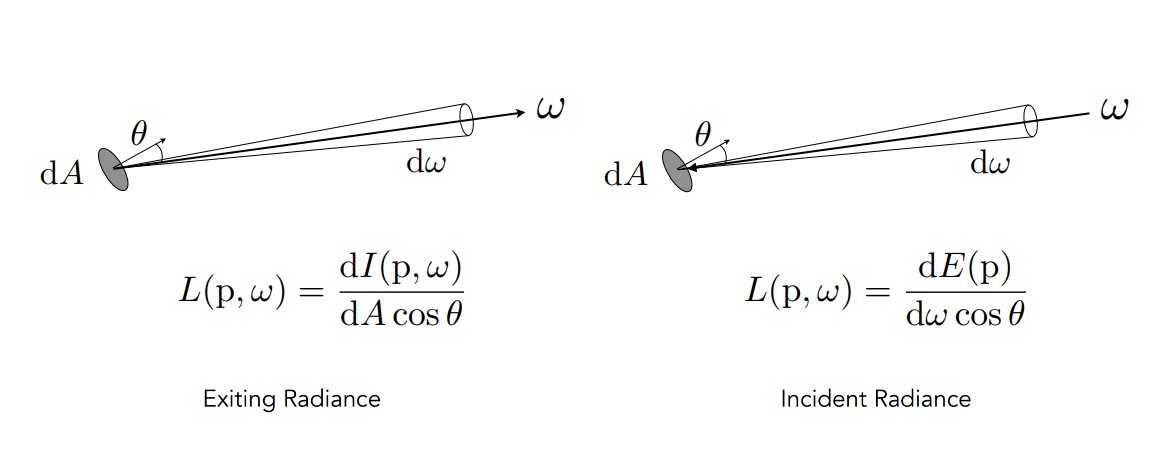
回过头来看一下 Radiant Intensity和Irradiance以及Radiance三者的定义

  • Radiant Intensity：每立体角发射的功率
  • Irradiance：每单位面积接收的功率
  • Radiance：每单位面积从每立体角接收的功率

那么就可以得到

  • Radiance：Radiant  Intensity / 单位面积
  • Radiance：Irradiance / 立体角

但这里有一个细微的区别，在irradiance中定义的每单位照射面积，而在radiance当中，为了更好的使其成为描述一条光线传播中的亮度，且在传播过程当中大小不随方向改变，所以在定义中关于接收面积的部分是每单位垂直面积，而这一点的不同也正解释了图中式子分母上的cosθ，具体可以观察如下图：

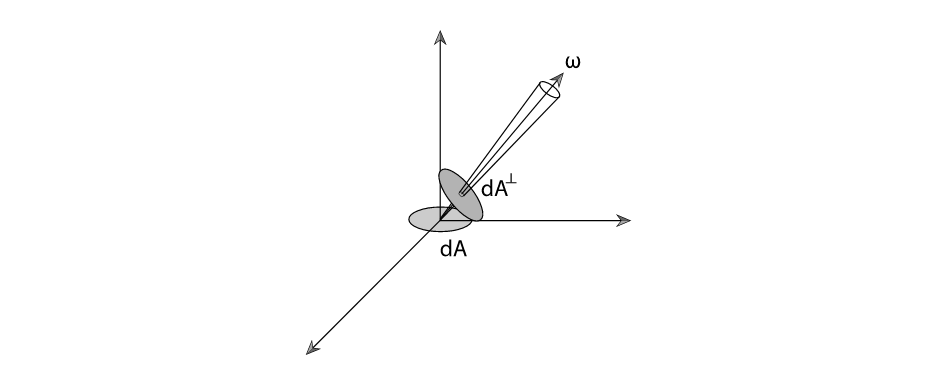
即图中的dA是irradiance中定义所对应的，而 dA⊥ 才是radiance中所定义的面积。二者之间的关系为

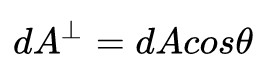
在理解了radiance和irradiance的定义之后，再讨论讨论它们之间的关系，通过二者的定义式子，不难得出如下结果：

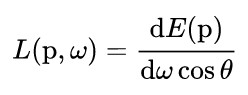
进一步推导得到：

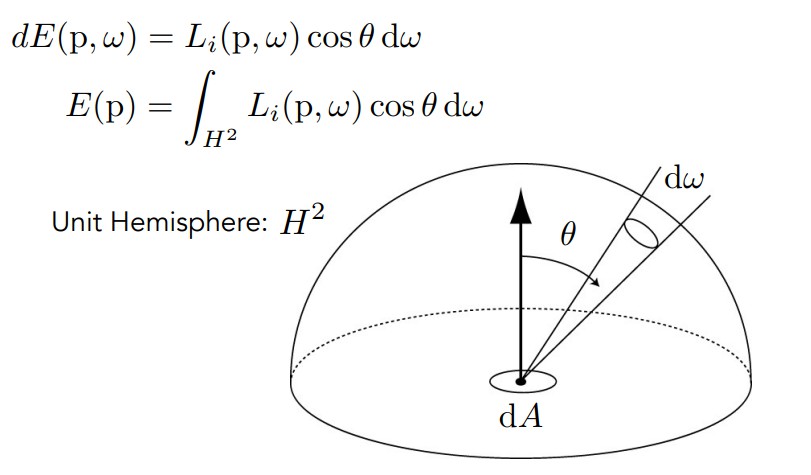
观察一下积分后的式子，E(p)就是点p的irradiance，其物理含义是上文所提到过的点p上每单位照射面积的功率，而Li(p,w)指入射光每立体角，每垂直面积的功率。

因此积分式子右边的cosθ解释了面积上定义的差异，而对dw积分，则是相当于对所有不同角度的入射光线做一个求和，那么该积分式子的物理含义便是，一个点(微分面积元)所接收到的光线亮度(irradiance)，由所有不同方向（立体角）的入射光线亮度(radiance)共同贡献得到。

 

双向反射分布函数(BRDF)

所谓BRDF（Bidirectional Reflectance Distribution Function，双向反射分布函数），指的是从辐射度量学的角度去理解光线的反射，如下图所示：

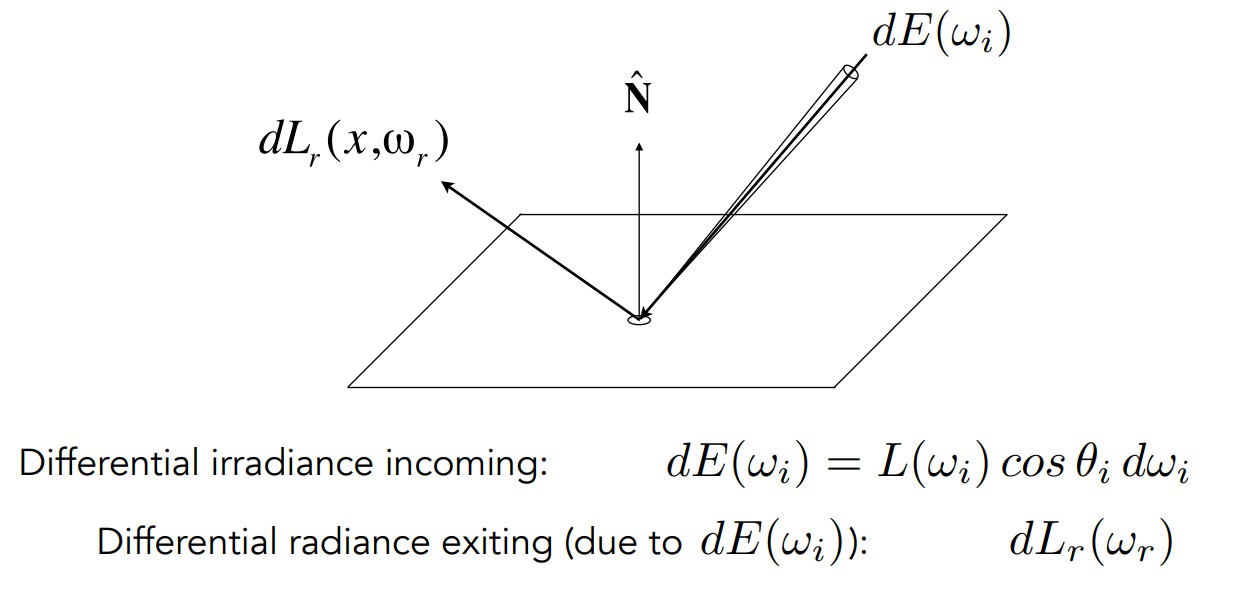
反射就是一个点(微分面积元)在接受到一定方向上的亮度dE(ωi)之后，再向不同方向把能量辐射出去dLr(ωr)。

从直观的理解来说，不同材质的表面自然会把一定方向上的入射光线反射到不同方向上，如理想光滑表面会把入射光线完全反射到镜面反射方向，其它方向则完全没有；而理想粗糙表面会把入射光线均匀的反射到所有方向。

因此所谓BRDF就是描述这样一个光线从不同方向入射之后，反射光线的分布情况的函数，定义如下：

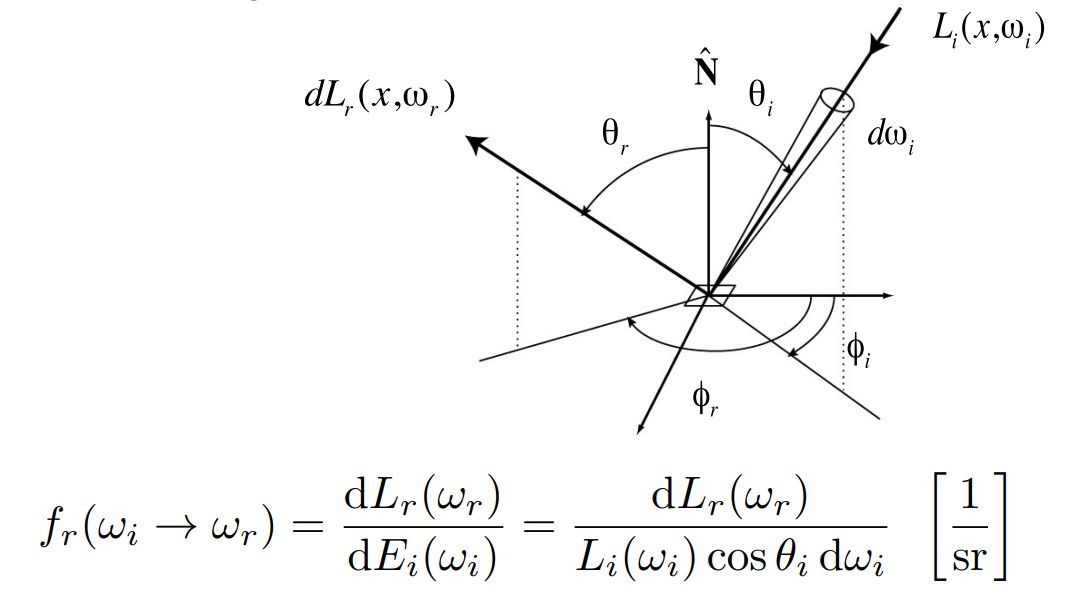
上图中下方的式子即为BRDF，它接收两个参数，入射光方向ωi，反射光方向ωr，函数值为反射光的radiance与入射光的iiradiance的比值。(从某个方向接受到的光能有多少反射到另外一个方向。)

 

BRDF的性质

1.BRDF是非负的（Non-negativity），表示了能量的分布

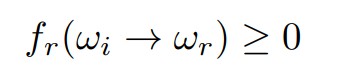
2.BRDF是线性的（Linearity），可以拆分和叠加

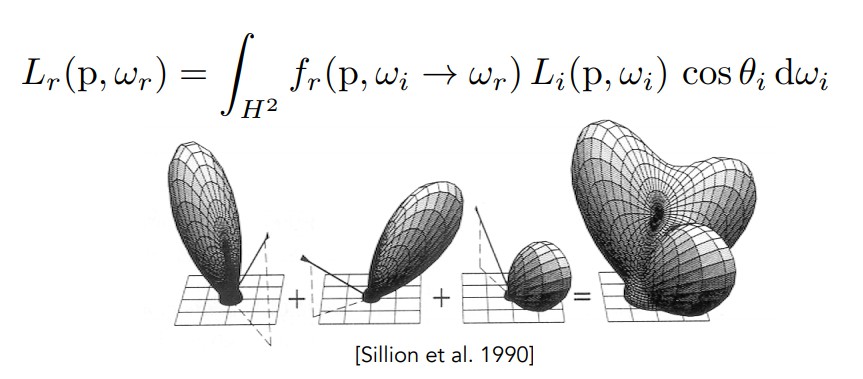
3.BRDF是可逆的（Reciprocity principle），调换入射方向和出射方向依然成立

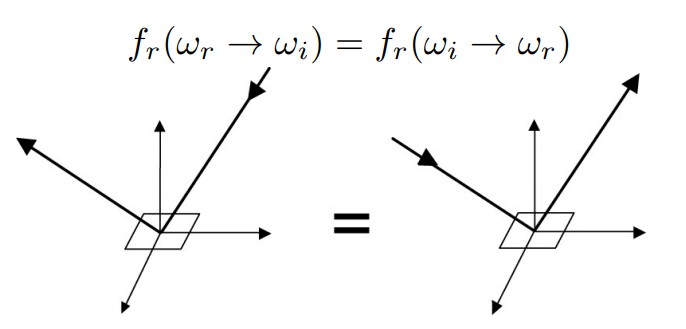
4.BRDF满足能量守恒（Energy conservation），入射能量等于反射能量（存在能量吸收的情况时，入射能量大于反射能量）。

 

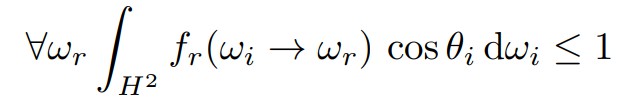
反射方程

借助BRDF，可以定义出反射方程如下：

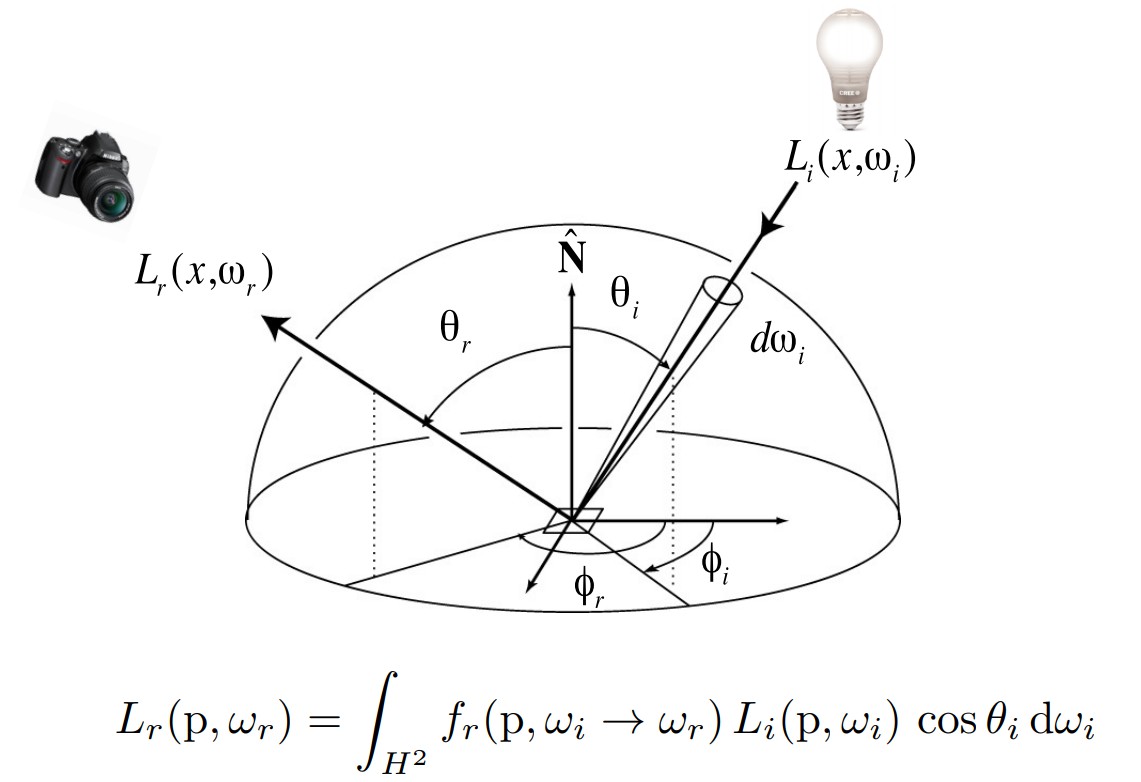
即摄像机所接受到的ωr方向上的反射光，是由所有不同方向上入射光线的irradiance贡献得到的(即图中式子的Li(p,ωi)cosθidωi)，而不同方向入射光线的irradiance对反射方向ωr的贡献程度则由物体表面材质决定，所以乘上了一个BRDF函数。

到这里，通过辐射度量学，以及BRDF最终得到的反射方程正是一个完全正确的光线传播模型了，解决了在光线追踪算法的所有缺点！（渲染方程只是在反射方程的基础之上加了一个自发光项，下面会详细介绍)。

在进入到渲染方程之前，再仔细观察一下反射方程：

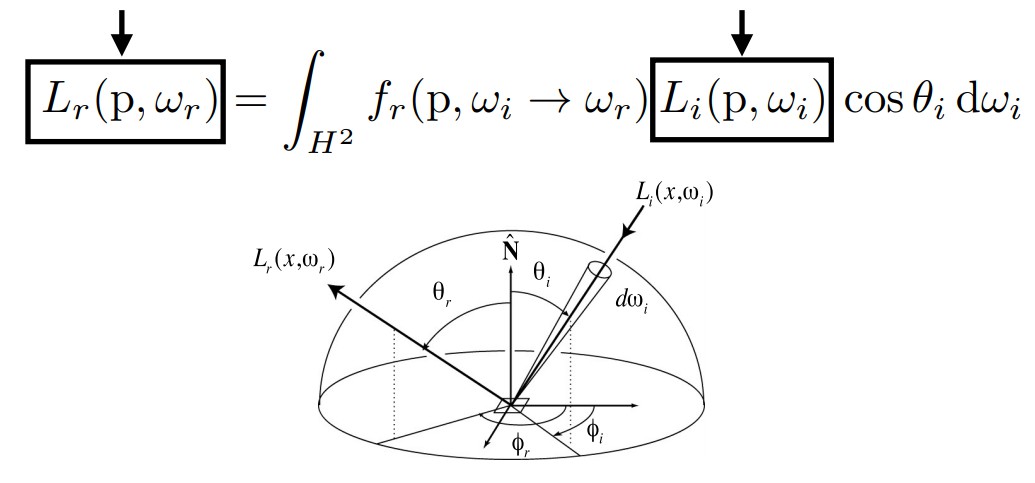
不难发现正如上图中所说的，入射光线的radiance不仅仅是光源所引起的，还有可能是其他物体上着色点的反射光线的radiance，恰好反射到当前的着色点p(即间接光照)，同时其他物体上的反射光线的radiance依然也是由直接光照和间接光照构成，因此这与whitted-style当中的光线追踪过程十分类似，也是一个递归的过程。所以说想要解这样一个方程还是比较难的。

 

渲染方程

渲染方程只是在反射方程的基础之上添加了一个自发光项(Emission term)，从而使得反射方程更加的通用，适用于所有物体表面上的光线传播问题：

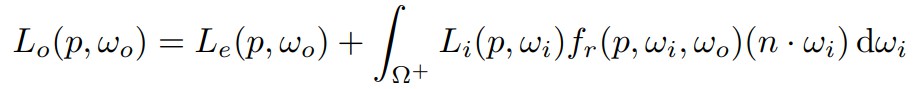
其中Le(p,ω0)为自发光项，反射方程中的cosθ用n·ωi代替 (所有光线方向均以从平面向外为正方向)。

接下来从不同的场景去理解渲染方程，首先从一个点光源和单个物体的场景：

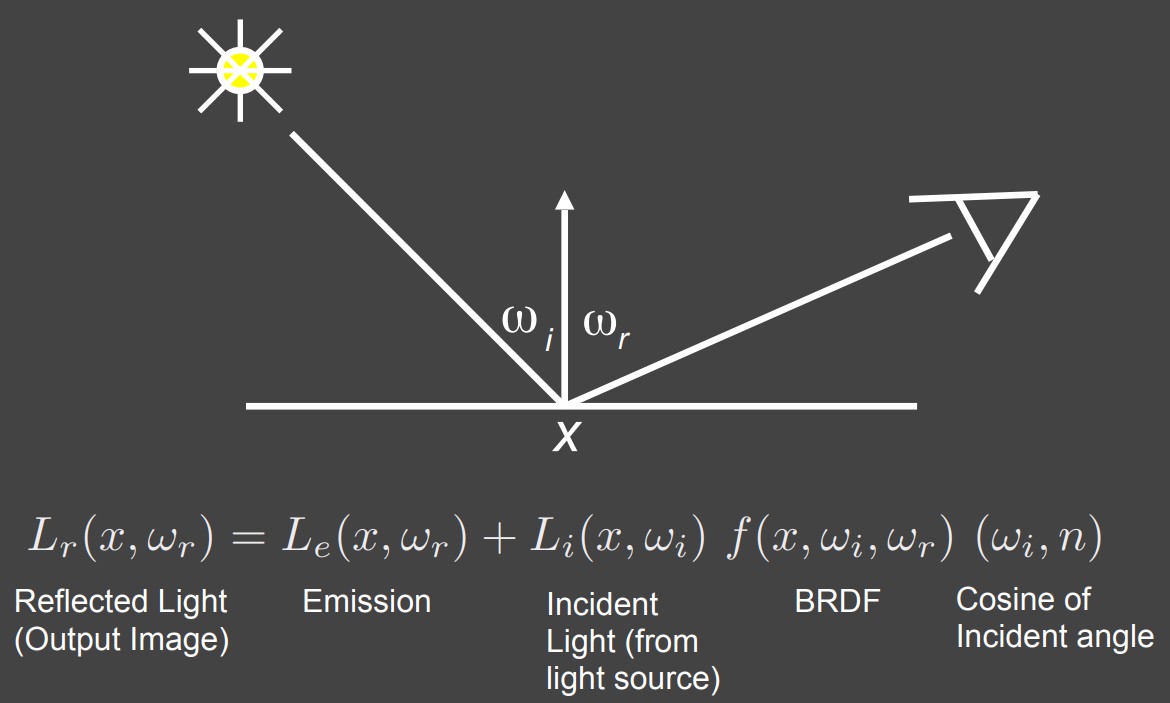
点光源对一个点来说自然只有一个方向有入射光，所以这里没有了积分。

多个点光源一个物体的场景：

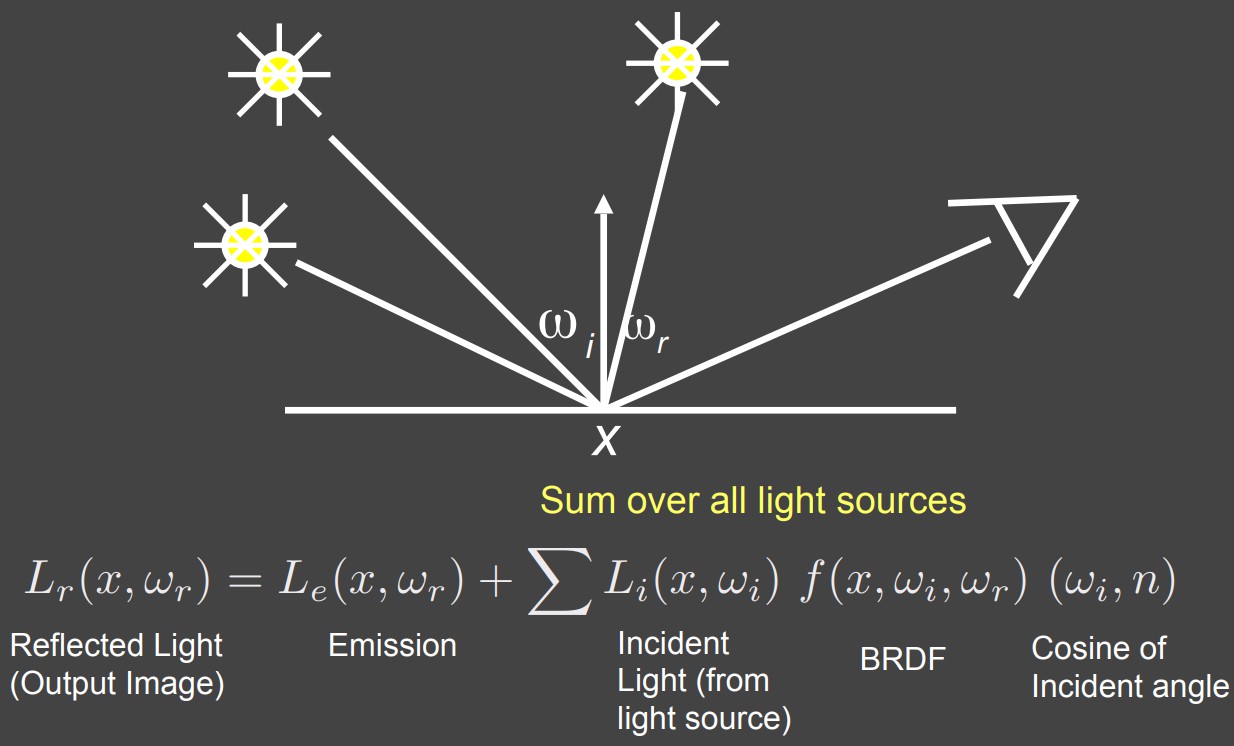
将所有的点光源的贡献全部求和即可，那么如果点光源变成了面光源呢？：

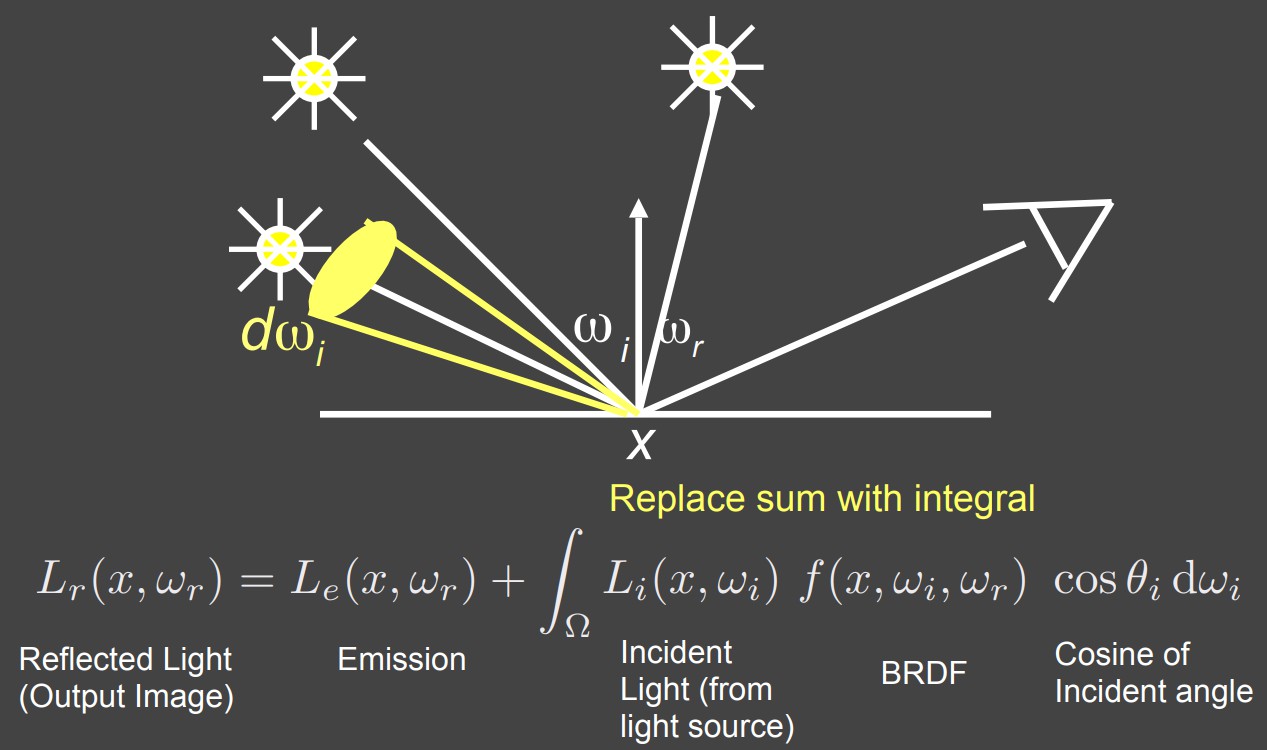
其实面光源就相当于无穷多个点光源的集合，只需要对面光源所在的立体角范围进行积分，并且能够确定不同立体角方向的面光源的入射光线radiance即可。

那么更进一步的，再在场景当中加入其它物体，使得物体之间发生光线交互之后是什么情况呢：

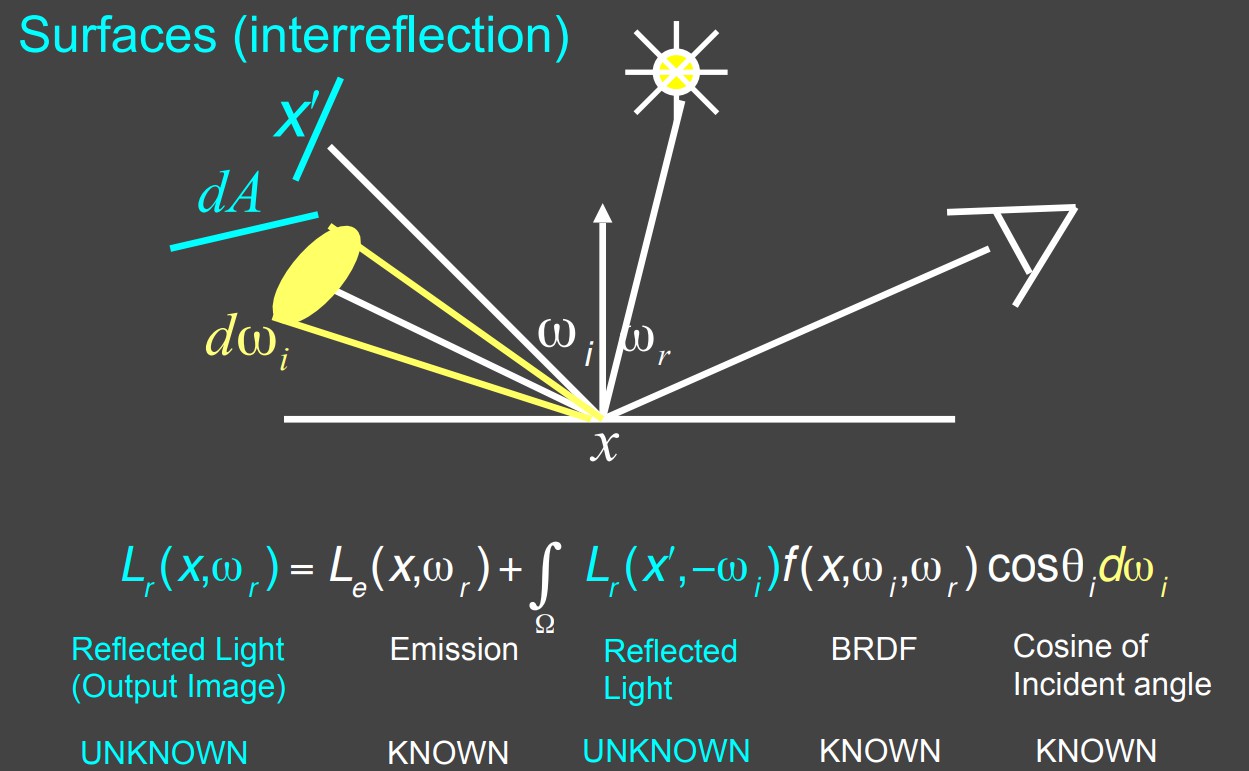
如上图所示，可以把其它物体同样考虑成面光源，对其所占立体角进行积分即可，只不过对其它物体的立体角积分不像是面光源所有入射方向都有radiance，物体的立体角可能只有个别几个方向有入射的radiance(即多次物体间光线反射之后恰好照射到着色点x)，其它方向没有，但本质上都可以视作是面光源。

观察一下图中的渲染方程可以发现除了两个radiance，其它所有项都是知道的，可以将上式进一步写成如下图下方所示的式子：

其中各项与原渲染方程中一一对应，(这里其实是有数学严格推导的，不过我们只是为了接下来构建直观的物理解释，对于这些推导不必在意，默认成立即可)，再接着，可以把该式子离散化写为线性代数的形式：

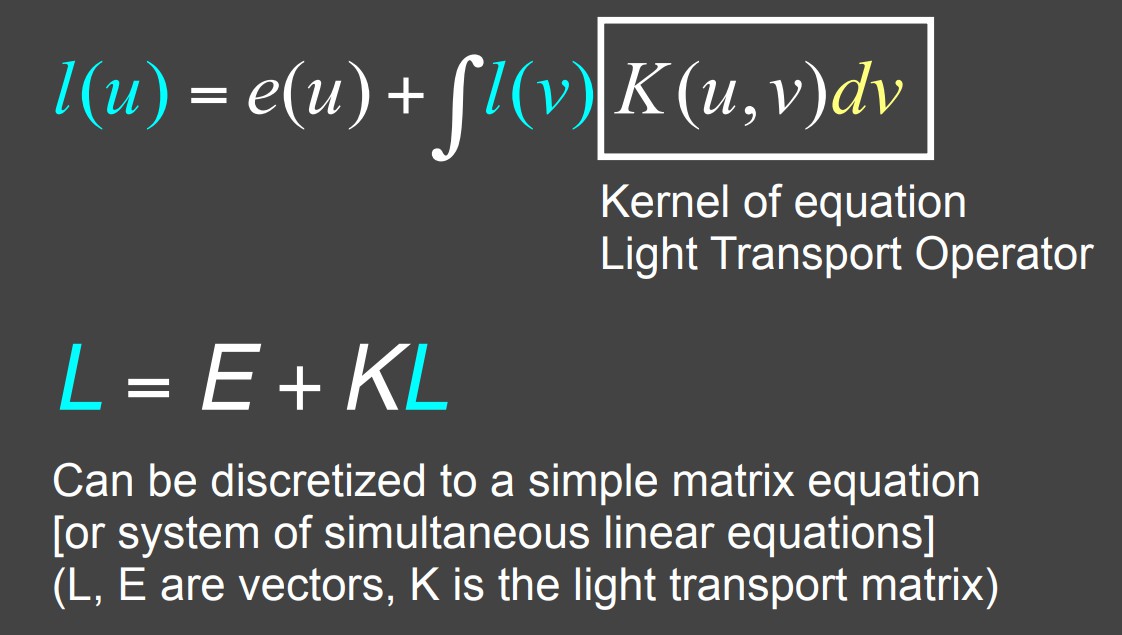
经过两步我们不是很清楚但其实是正确的数学推导之后，得到了这样一个递归式：

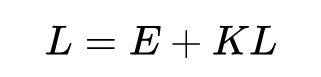
其中L其实就是想要求得的反射光，E是自发光其实就是光源的发光项，K可以理解为对光线进行反射的一种算子操作(因为它由BRDF转化来的)。那么利用线性代数的知识很容易就可以推导出L的结果如下：

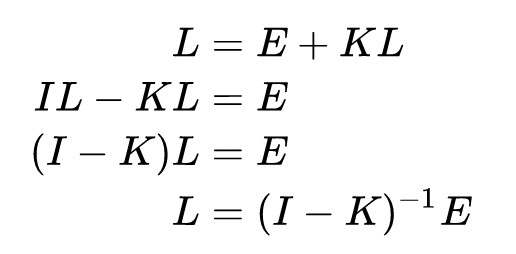
其中I为单位矩阵，再接着使用广义二项式定理得到：

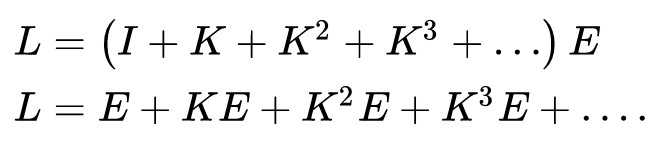
仔细观察这个式子，注意E是光源所发出的光，K为反射算子，这样一个式子的物理含义如下图所示：

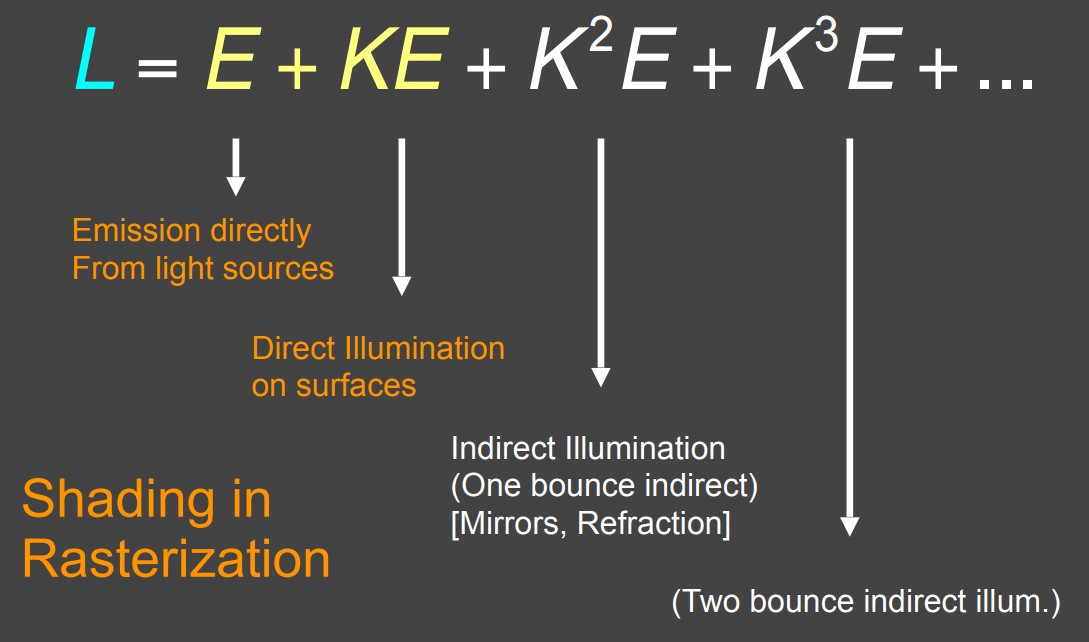
E为光源发出的光，KE则代表对光源反射一次的结果，即直接光照，那么前两项之和就是光栅化当中着色所考虑的结果，对于全局光照来说，还考虑了第三项KKE，即一次弹射的间接照明，KKKE就是两次弹射的间接照明，依次类推。

这样来看整个结果就很清晰了，就是光源发光加上直接光照与多次间接光照的结果！而这一切都是从渲染方程推导而来的，因此这也正是渲染方程的物理意义！

不同弹射次数下同一场景的渲染效果如下，可右键打开大图查看

显然弹射次数越多越接近真实图片效果，但提升幅度逐渐递减。

 

本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》和孙晓磊的计算机图形学系列笔记，感谢。

每天清晨有多少双眼睛睁开，
有多少人的意识苏醒过来，
便有多少个世界。

《追忆似水年华》
——马赛尔·普鲁斯特