前言

在上一篇文章中说过Lambert光照模型的原理和实现方式，Lambert只能模拟粗糙平面的漫反射现象，没法模拟光滑平面的高光反射。

想要模拟高光反射就不得不提经典的Phong光照模型，在Lambert漫反射模型的基础上，增加了模拟高光反射的算法，再叠加上环境光和自发光，可以比较真实地模拟常见的光照效果。

后来又出现了Blinn-Phong的光照模型，与Phong的区别就是对高光反射的计算方式进行了一定优化。

因此本文就介绍一下这两种光照模型中高光反射部分的计算原理以及在Unity和UE4中模拟实现的方法。

 

高光原理

首先请看下图，联想一下用镜子反射阳光或者灯光的时候，高光亮度是与观察角度有关的，当从光线反射方向观察时高光亮度最大，这就是Phong光照模型的技术原理。

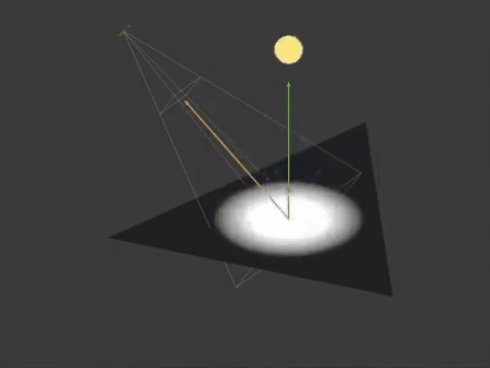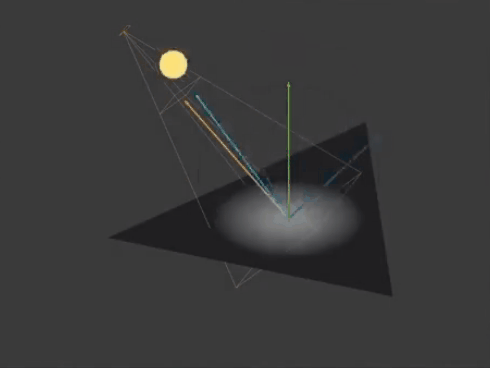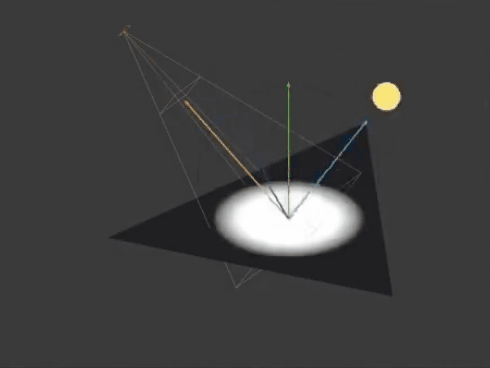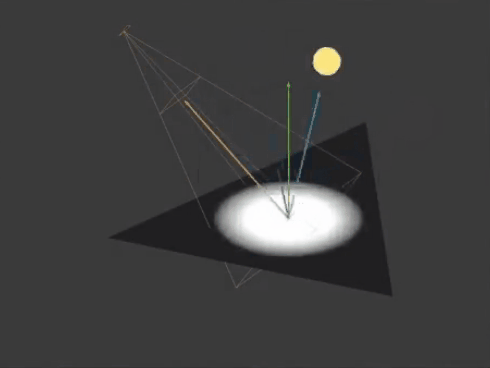
而高光强度的计算方式正是通过求光线反射方向rDir和观察方向vDir的点积得到，即dot(rDir, vDir)。

另外一种计算方式则是通过求光线反方向lDir和观察反射方向vrDir的点积得到，即dot(lDir, vrDir)。这种计算方式可以通过下图理解。

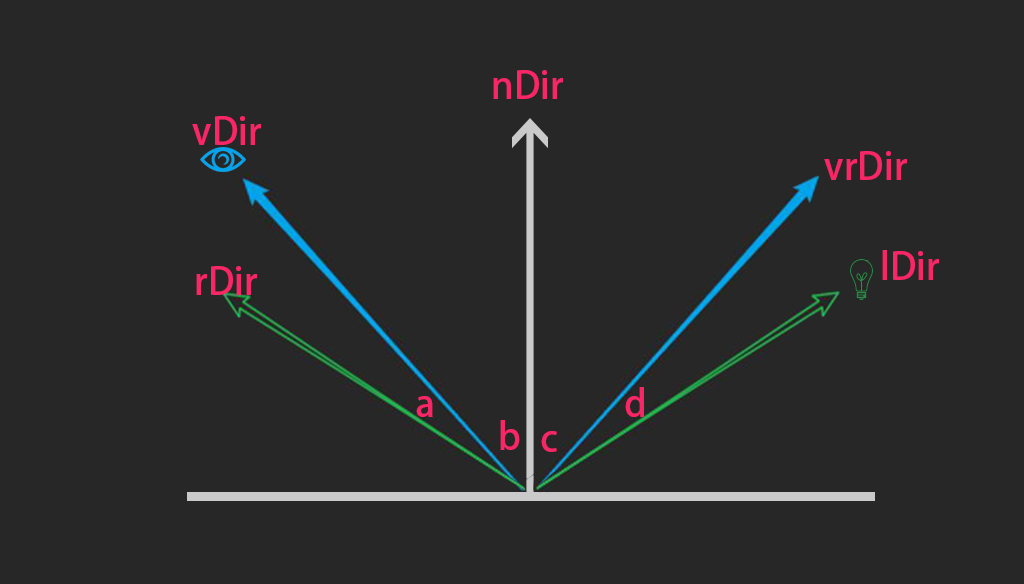
而Blinn-Phong光照模型的高光亮度计算方式则是通过计算法线方向nDir和半角方向hDir（光照方向lDIr与观察方向vDir的中间角）的点积得到，即dot(nDir,hDir)。

Blinn-Phong光照模型是在Phong上的简化，胜在多数情况下计算速度快效果也不错，因此在早期计算机性能不够的时候被大量使用，而如今已经可以自由选择不同模型进行高光计算了。

 

在Unity中模拟Phong以及Blinn-Phong的高光反射

phong的高光反射可通过以下节点连接进行模拟。

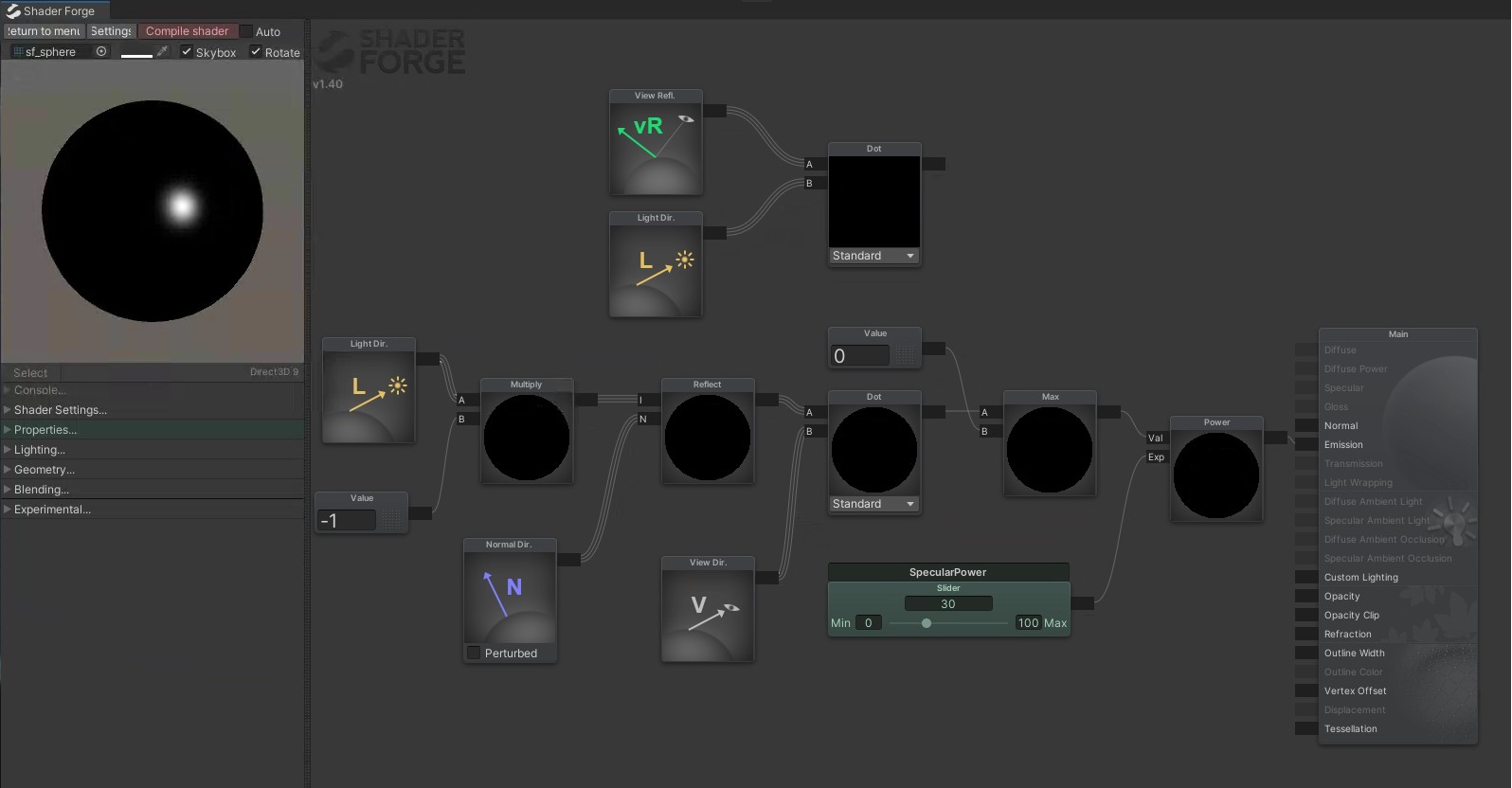
其中Power节点为n次幂节点，n越大，会导致高光范围越小。

Blinn-Phong的高光反射则可以通过以下方式实现。

 

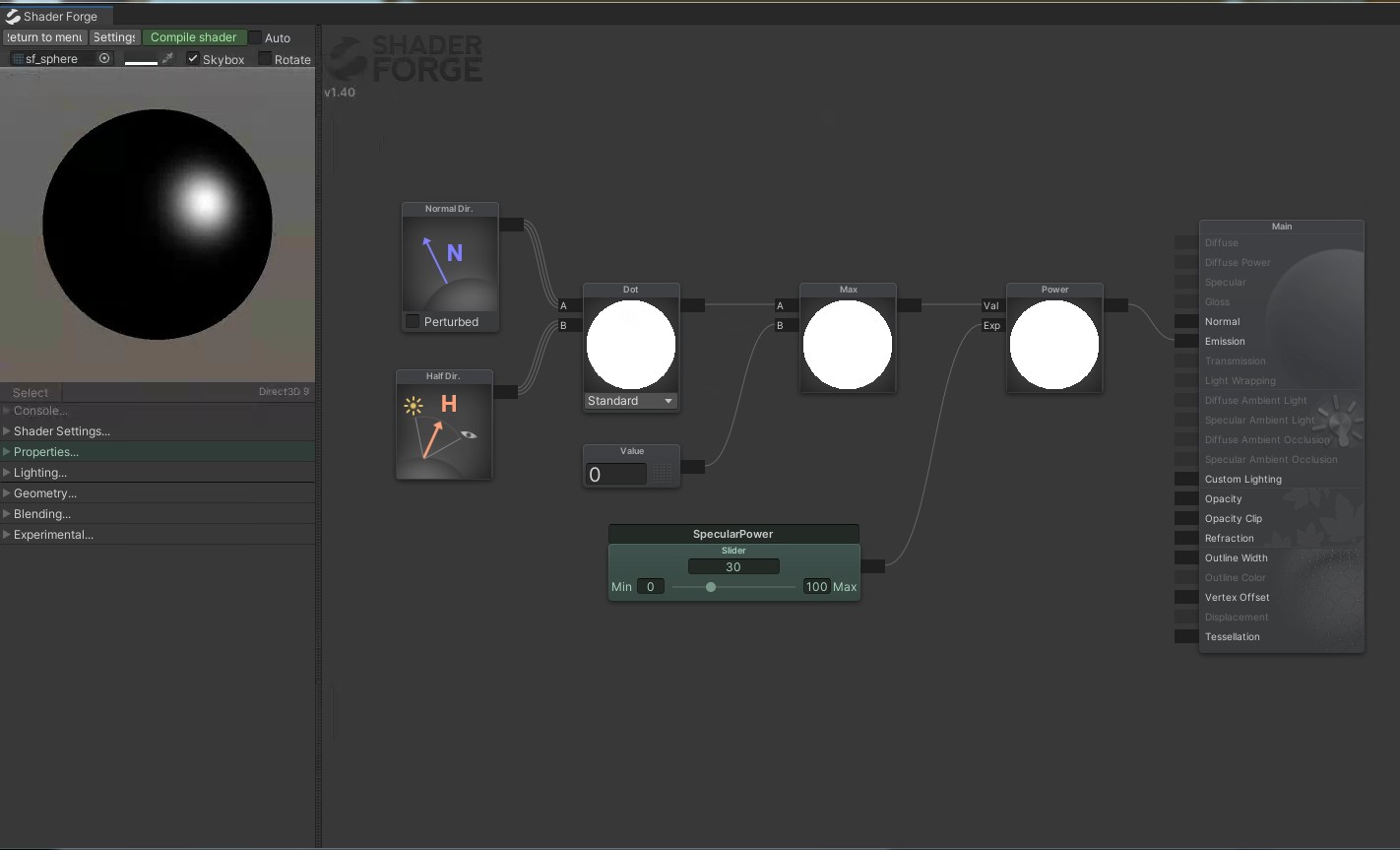
在UE4中模拟Phong以及Blinn-Phong的高光反射

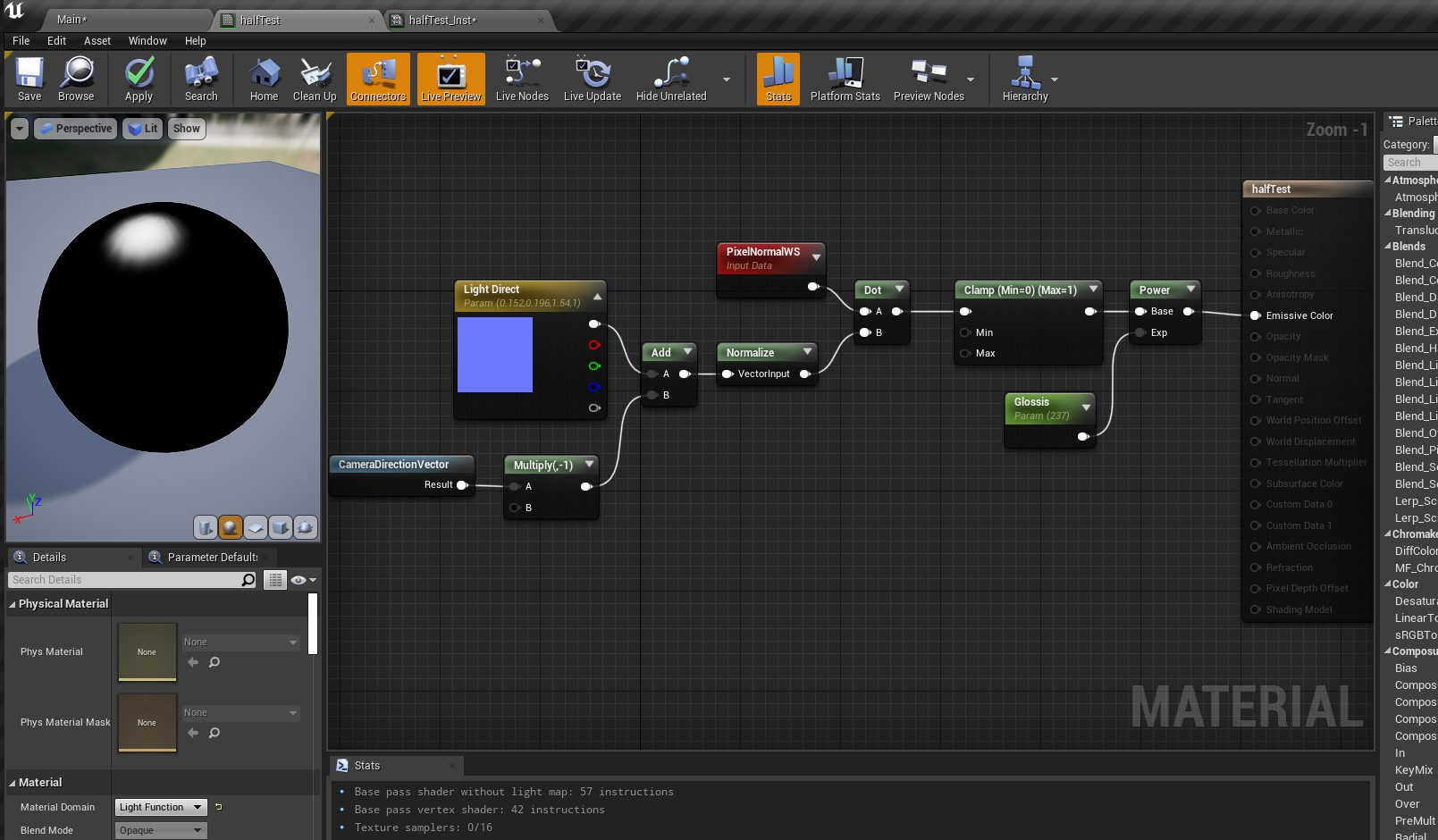
在UE4中可以通过以下方式模拟Phong的高光反射

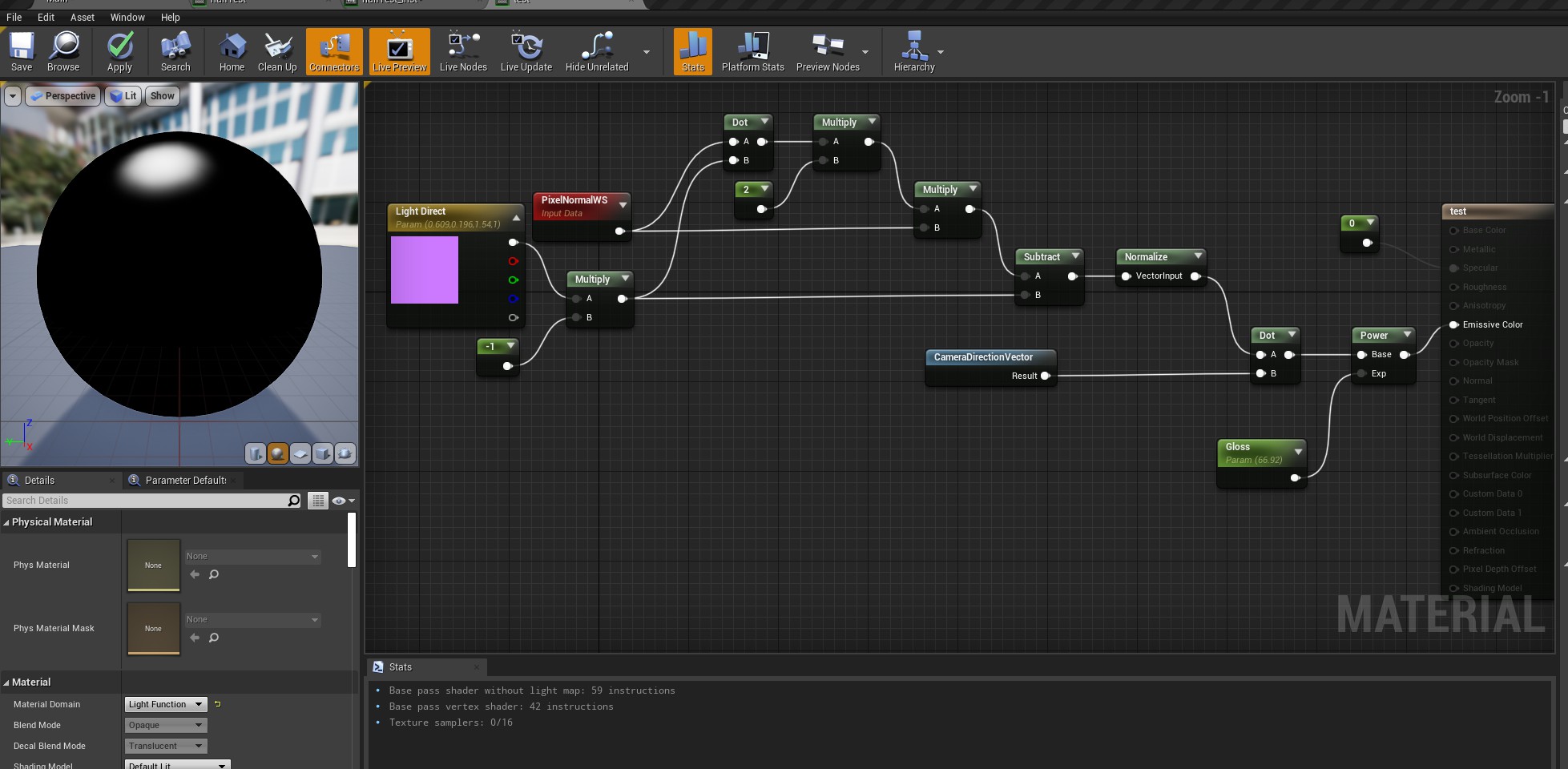
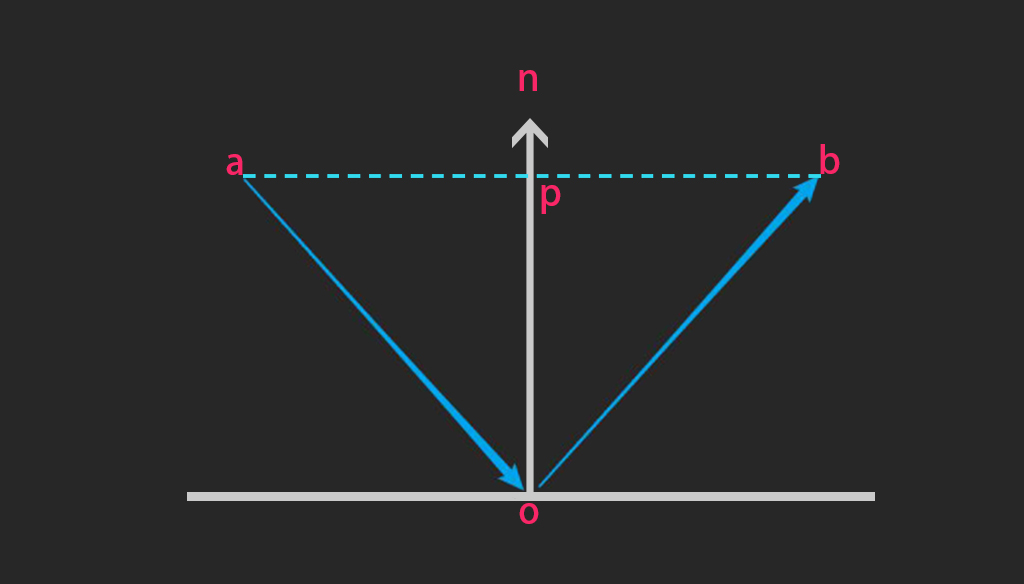
其中光线反射rDir的求证方式比较复杂，参考下图，其中ao为光线方向，求光线反射ob可以转化成ab-ao，进而2ap-ao，再转化成 2(ao+op)-ao，也就是ao+2op，而前文说过点积的数学意义即是cos余弦值，因此可以通过oa和法线on的点积得到op，具体过程可参考几何向量：计算光线反射reflect向量。

而Blinn-Phong光照模型的高光则如下：

 

在Unity中通过代码实现Phong和Blinn-Phong

代码如下，不只是高光反射部分的代码，还与Lambert整合在一起，最终输出的是拥有漫反射和高光反射，并且能反应灯光颜色的简易shader。

如果再加上自发光和环境光的话就是完整的Phong和Blinn-Phong光照模型了。

// shader的路径和名称
Shader "Shader Forge/phong" {
    // 自定义暴露到控制面板的属性
    Properties {
        _BaseColor ("Base Color", color) = (0.7, 0.4, 0.4, 1.0)
        _SpecularPow ("Specular Power", range(1,90)) = 30
    }
    SubShader {
        Tags {
            "RenderType"="Opaque"
        }
        Pass {
            Name "FORWARD"
            Tags {
                "LightMode"="ForwardBase"
            }
            
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag
            #include "UnityCG.cginc"
            #pragma multi_compile_fwdbase_fullshadows
            #pragma target 3.0
            
            // 声明变量
            uniform float4 _LightColor0;
            uniform float3 _BaseColor;
            uniform float _SpecularPow;
            
            // 输入结构
            struct VertexInput {
                // 输入顶点的物体空间位置
                float4 vertex : POSITION;
                // 输入物体空间法线
                float3 normal : NORMAL;
            };
            
            // 输出结构
            struct VertexOutput {
                // 输出顶点的裁剪空间位置
                float4 posCS : SV_POSITION;
                // 输出顶点的世界空间位置
                float3 posWS : TEXCOORD0;
                // 输出法线的世界空间方向
                float3 nDirWS : TEXCOORD1;
            };
            
            // 顶点shader
            VertexOutput vert (VertexInput v) {
                VertexOutput o = (VertexOutput)0;
                // 计算法线的世界空间方向
                o.nDirWS = UnityObjectToWorldNormal(v.normal);
                // 计算顶点的裁剪空间位置
                o.posCS = UnityObjectToClipPos( v.vertex );
                // 计算顶点的世界空间位置
                o.posWS = mul(unity_ObjectToWorld, v.vertex);
                return o;
            }
            
            // 像素shader
            float4 frag(VertexOutput i) : COLOR {
                // 准备向量
                float3 nDirWS = i.nDirWS;
                float3 lDirWS = normalize(_WorldSpaceLightPos0.xyz);
                float3 vDirWS = normalize(_WorldSpaceCameraPos.xyz - i.posWS.xyz);
                float3 hDirWS = normalize(vDirWS + lDirWS);
                // float3 rDirWS = reflect(-lDirWS,nDirWS);  // phong模型所需的光线反射方向
                
                // 计算点积
                float nDotl = dot(nDirWS, lDirWS);
                float nDoth = dot(nDirWS, hDirWS);
                // float vDotr = dot(vDirWS, rDirWS);  // phong模型所需的点积
                
                // 光照模型
                float LambertIntensity = max(0.0,nDotl);
                float BlinnPhongIntensity = pow(max(0.0, nDoth), _SpecularPow);
                // float PhongIntensity = pow(max(0.0, vDotr), _SpecularPow);  // phong模型的亮度
                float3 FinalRGB = _BaseColor.rgb * LambertIntensity * _LightColor0.rgb + BlinnPhongIntensity * _LightColor0.rgb;
   
                return float4(FinalRGB, 1.0);
            }
            ENDCG
        }
    }
    FallBack "Diffuse"
}

本文同样参考自B站庄懂的技术美术入门课，感谢。

 

我们的尊严不值什么钱，
可它是唯一我们真正拥有的东西，
是我们最后一寸领土，
但在那一寸领土里，
我们是自由的。

——《V字仇杀队》