前一篇写了向量的基础运算及应用,这一篇就轮到矩阵了。
矩阵
首先来说一下矩阵的基础概念。
由m×n个数排成的m行n列的数表称为m行n列的矩阵,简称m×n矩阵。记作:

矩阵的加减运算方法是同位置的元素的相加减,因此加减运算时行数和列数必须相同,例如
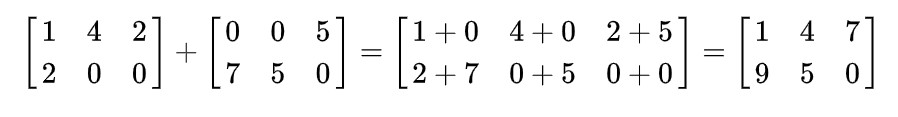
数乘矩阵则是数和矩阵的每一个元素相乘。
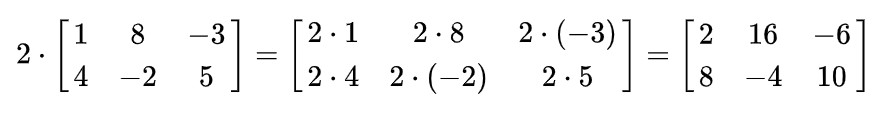
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵,这一过程称为矩阵的转置。
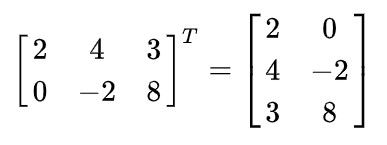
矩阵的转置满足以下规律
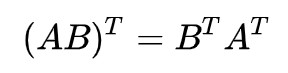
当矩阵的转置等于它自身,即矩阵沿左上-右下对角线对称时,该矩阵就被称为对称矩阵,例如
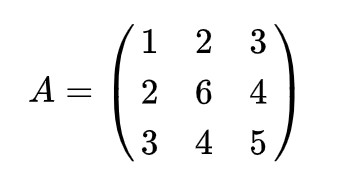
而当对角线处的元素都为1,其他元素都为0时,该矩阵则被称为单位矩阵,例如
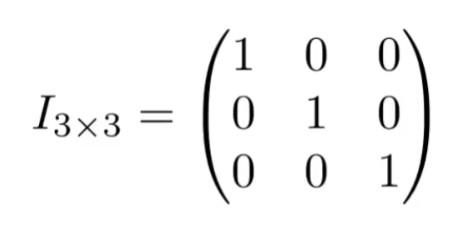
矩阵的乘法
矩阵的乘法比较特殊,A和B能进行乘法的前提是A的列数等于B的行数,最后得到的结果矩阵C的行数和A矩阵相同,列数和B矩阵相同,即(M x N)(N x P) = (M x P)。
对于相乘结果第i行第j列的元素,计算方式及示例如下
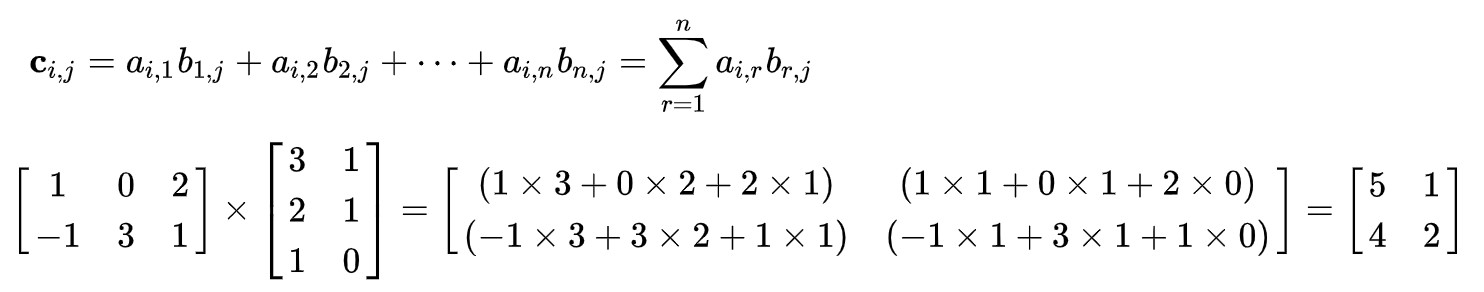
这个计算方式可以理解为A矩阵的第i行点乘B矩阵的第j列。
显然矩阵的乘法不满足交换律,但满足结合律和分配率。
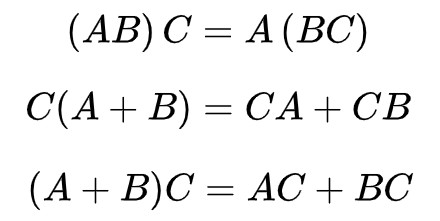
当A矩阵乘以单位矩阵时,结果仍是A矩阵本身;而当A矩阵与B矩阵的乘积是单位矩阵时,则称A和B互逆,是对方的逆矩阵。
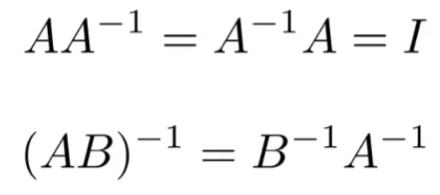
向量与矩阵的关联
在前文中说过,在计算机图形学中一般把向量写成纵向的列向量,或者说是向量的转置,此时可以当做一个n行1列的矩阵,进行矩阵的运算。
例如对一个点的二维坐标进行沿y轴的对称变换操作,只需要用一个特定的矩阵乘以该坐标即可。
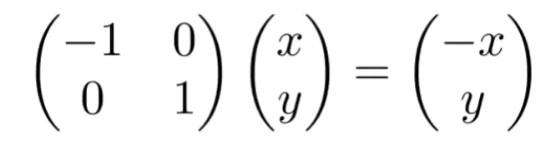
而向量的点乘也可以写成一个1行n列的矩阵与n行1列的矩阵相乘,最终结果当然是一个1行1列的常数。
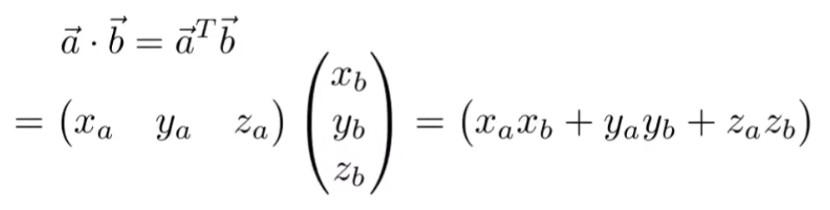
向量的叉乘也可以写成矩阵相乘形式如下
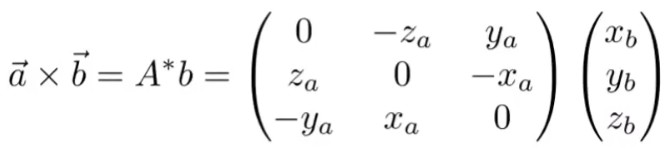
变换矩阵
变换矩阵 (Transformation Marices) 在图形学中的重要性不用多说,一切物体的缩放,旋转,位移,都可以通过变换矩阵得到。同时在投影 (projection) 变换的时候也有很多应用,下面会介绍一些简要的变换矩阵。
2D线性变换
将如下图所示的简单矩阵乘法定义为对向量(x,y)的线性变换,这样只要找到每个坐标变换对应的特定矩阵形式,就可以将坐标变换与矩阵计算联系起来。
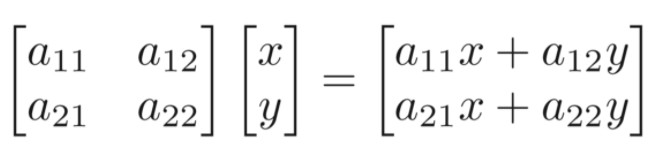
缩放(scaling)
缩放变换是一种沿着坐标轴作用的变换,定义缩放矩阵如下:
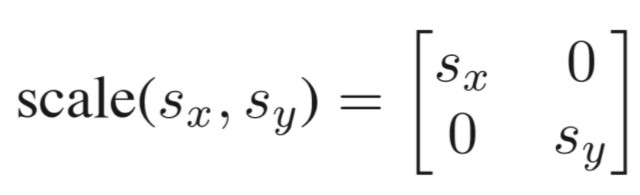
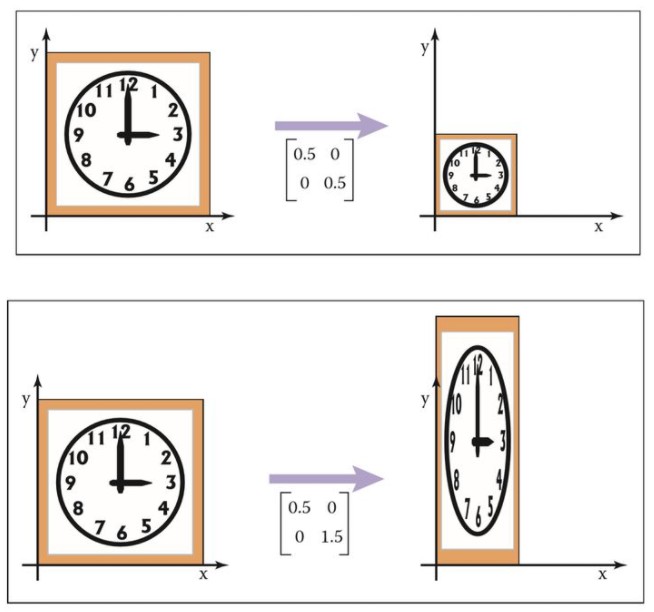
例如:
剪切(shearing)
所谓剪切就是把物体一边固定,另一边向侧方拉拽,剪切拉伸矩阵定义如下
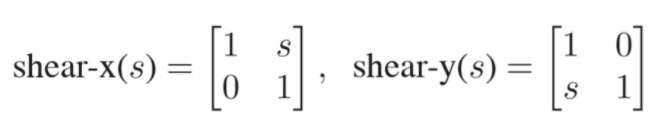
分别对应了x轴和y轴的拉伸
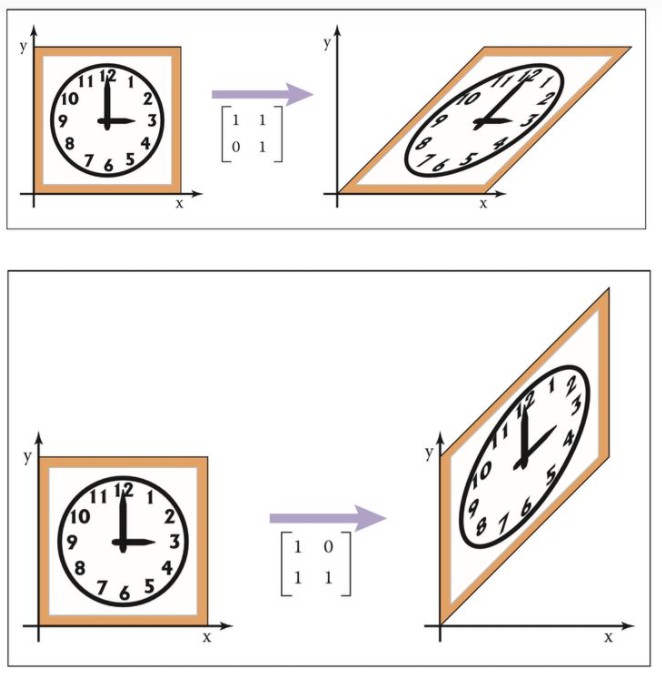
旋转(rotation)
沿原点旋转的变换矩阵要稍微复杂一下,定义如下
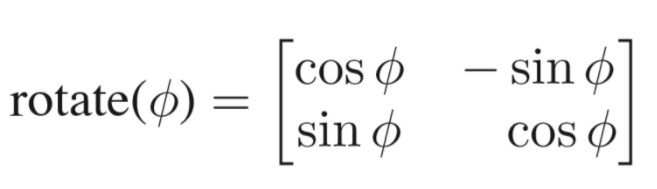
证明过程很简单,既然这个旋转变换矩阵对于图形上的每个点都成立,那么就找到几个特殊的点带入公式,求这个2×2矩阵的元素值。
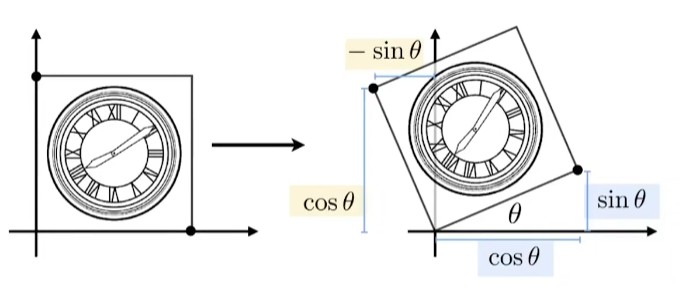
假定正方形边长为1,则右下角变换前坐标为(1, 0),变换后坐标为(cosθ, sinθ);而左上角变换前坐标为(0, 1),变换后坐标为(-sinθ, cosθ)。
然后将这两个点代入变换矩阵,即可求得。
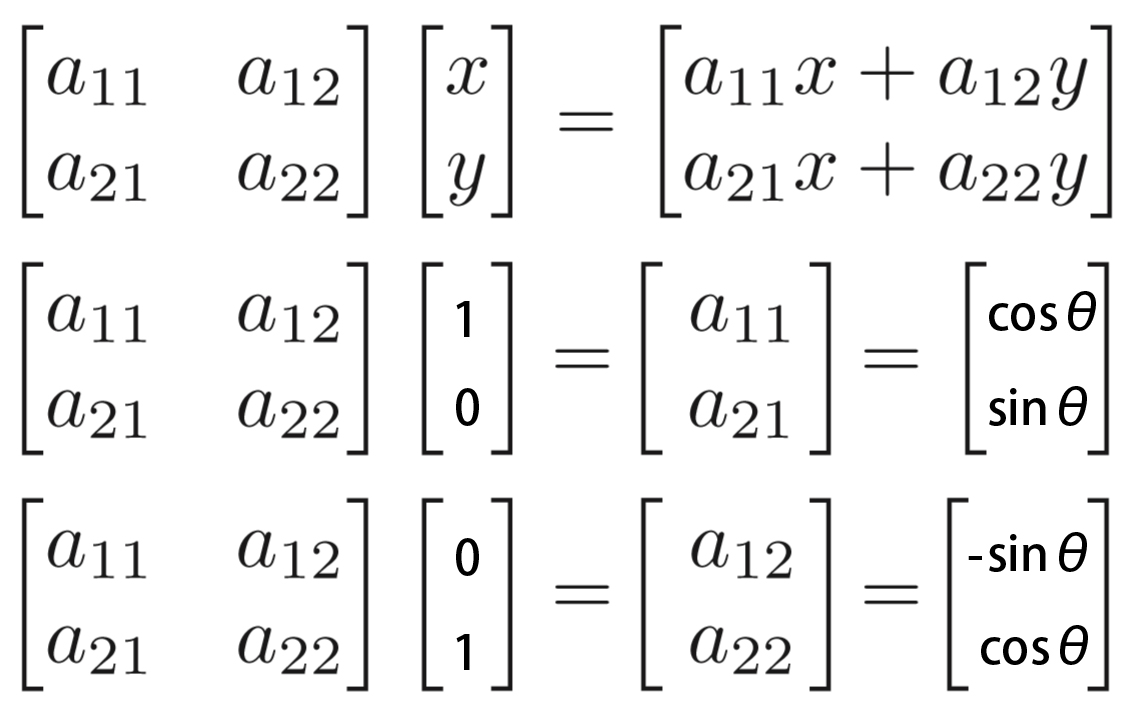
注意此时是将逆时针旋转视为正向角度,因此该矩阵就是逆时针旋转矩阵。
那么顺时针的旋转矩阵是什么呢?根据三角函数的规律,sin-θ = -sinθ,cos-θ=cosθ,可知,顺时针旋转矩阵如下
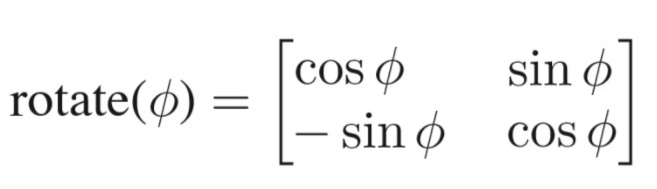
如果与逆时针旋转矩阵对比会发现,两者互为转置矩阵,而且互为逆矩阵,这种逆矩阵等于转置矩阵的情况数学上称为正交矩阵。
不止2D,扩展到更高维度的旋转矩阵也满足这一规则。
因此如果需要反向旋转,只需要将旋转矩阵转置再进行计算即可。
齐次坐标(Homogenous Coordinates)
刚才说了缩放、剪切和旋转,唯独没有说到平移。
乍一看,平移应该是最简单的坐标变换,可以很轻易的写成如下形式:
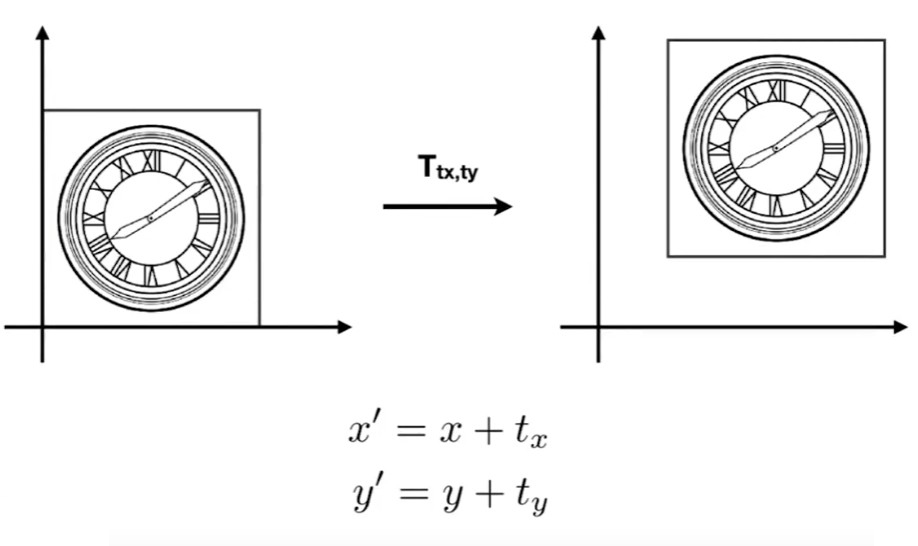
但如果要把它转换成线性变换矩阵则有些无从下手,不能写成和缩放旋转类似的矩阵相乘形式。为了让平移变换的形式与其他变换形式统一,于是引入了齐次坐标变换的概念。
所谓齐次坐标,就是给数据进行升维,二维点坐标(x, y)描述为(x, y ,1);二维向量(x, y)描述为(x, y ,0)。
这样,再回到刚才的位移变换中,就可以写成以下形式。
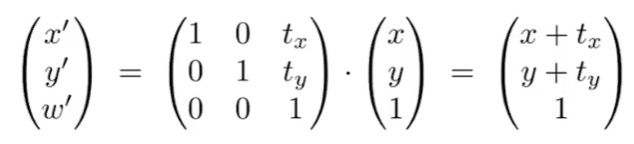
之所以区分点坐标和向量,是因为向量具有平移不变性,只有方向和长度的区别,与位置无关。这样,向量经过平移变换后不会被改变;同时两个点的坐标相减后,z坐标从1变为0,符合向量的定义。
齐次坐标还有一个重要的性质,就是数乘不变性,也就是(x,y,z,1)、(kx,ky,kz,k!=0)、(xz,yz,zz,z!=0)代表了三维空间中的同一个点(x,y,z),因此(x,y,z,1)+(a,b,c,1) = (x+a,y+b,z+c,2) = ((x+a)/2,(y+b)/2,(z+c)/2,1),这意味着齐次坐标下两个点相加等于两个点的中点。
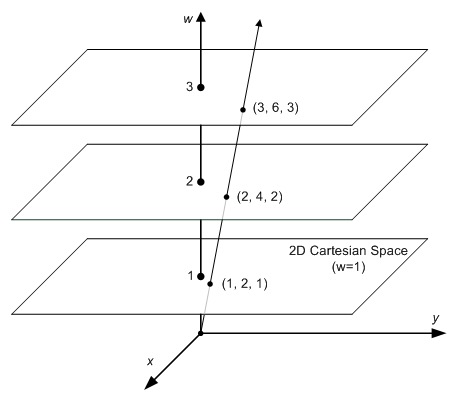
这就涉及到投影空间的概念了,之后有机会再单独开篇介绍。
这样一来,就可以将位移与rotation,scaling结合在一起,这种既有scale、rotation等,又有translation的变换,被称之为仿射变换(Affine Transformations)。
而2D线性变换的定义也就变成了下面这个形式。
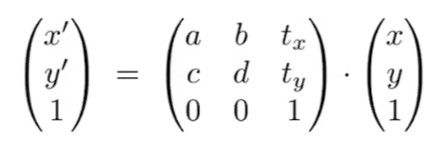

要注意的是,对于仿射变换,会先进行线性变换(即scale,rotation,shear这些),之后才会进行位移!因为前者是基于原点的,而位移会让图形离开原点。
而 对于多重变换来说,可以写成以下形式
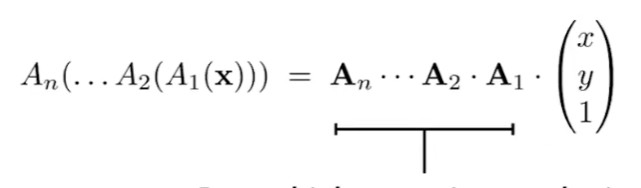
多个变换矩阵中,A1先和坐标进行计算,然后A2、A3,而由于矩阵乘法满足结合律,因此可以先将变换矩阵之间进行相乘,最后再乘以点坐标。这样再复杂的变换也可以汇总成一个变换矩阵来表示。
反过来说,既然可以组合,自然也可以进行分解。
例如沿某个点进行旋转,可以先平移图形到该点位于原点,再进行旋转,最后将图形反向位移回去。
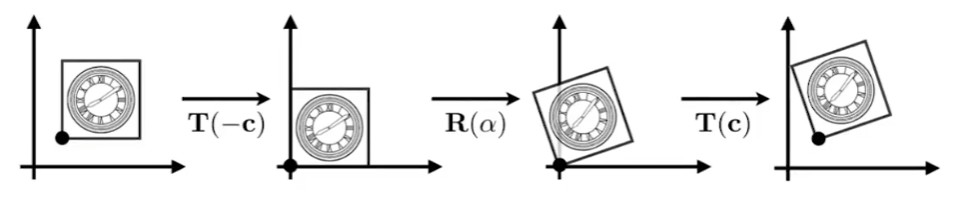
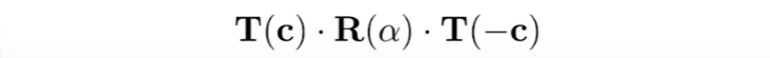
3D线性变换
从2D变换矩阵推算3D变换矩阵也比较简单。
3D缩放(scaling),3D剪切(shearing)
缩放很简单,依然是对角阵。
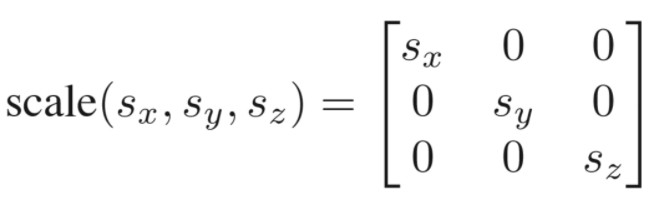
剪切也很类似
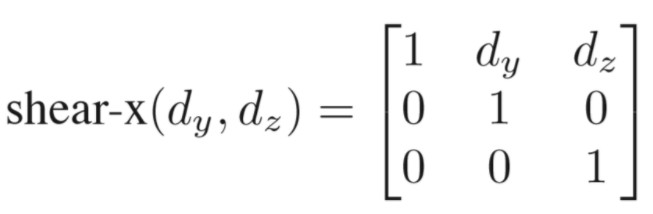
3D旋转(Rotation)
对于3D绕原点旋转来说一共有3类矩阵,分别对应绕x轴,y轴,z轴旋转!
由于采用的是右手系空间坐标,所以在二维之中逆时针旋转矩阵是x轴向y轴旋转,根据右手螺旋定则,对应到3维便是绕z轴旋转(x轴转向y轴),不难推出绕x轴旋转(y转向z),绕y轴旋转(z转向x)。
对应二维旋转矩阵能够类推得到三维旋转矩阵如下:
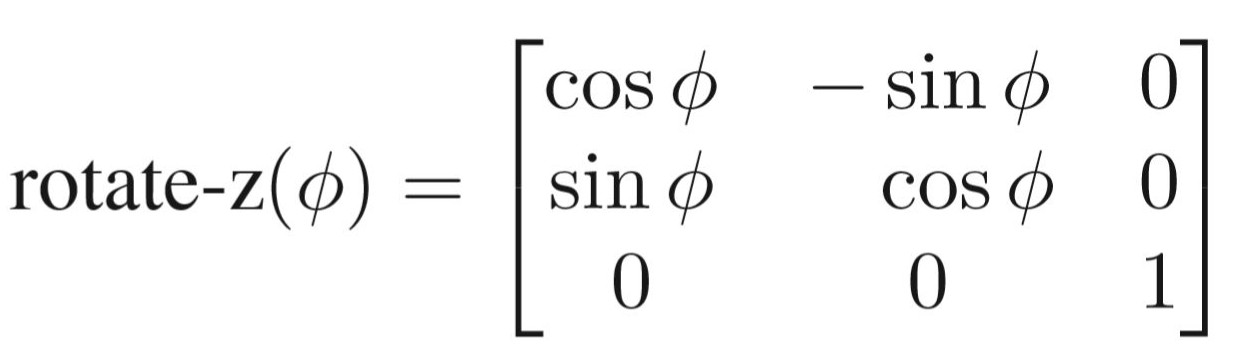
绕z轴,故z不变,且x转向y,左上角与二维逆时针旋转矩阵相同。
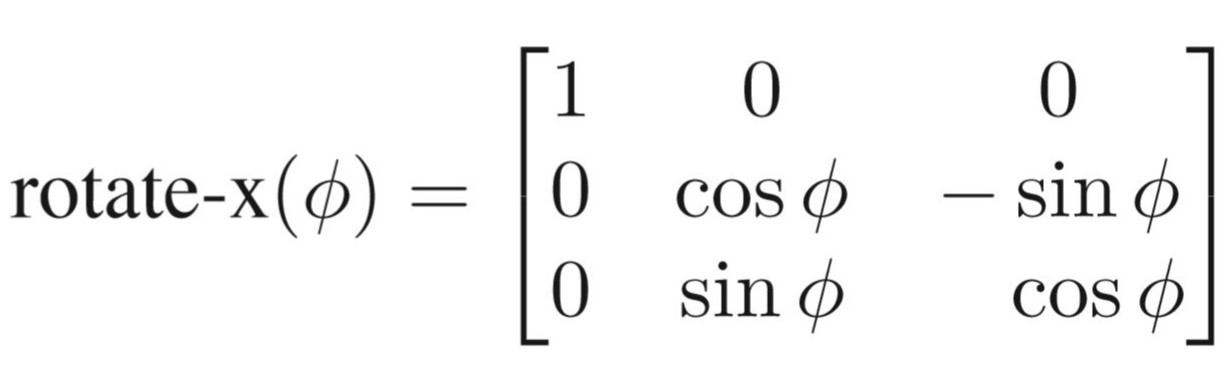
绕x轴,故x不变,且y转向z,右下角与二维逆时针旋转矩阵相同。
绕y轴会有一点不同,根据右手螺旋定则,绕y轴旋转是从z轴向x轴方向旋转,只要记住右手坐标系时,y轴=z叉乘x=-x叉乘z,很快就能反应过来。
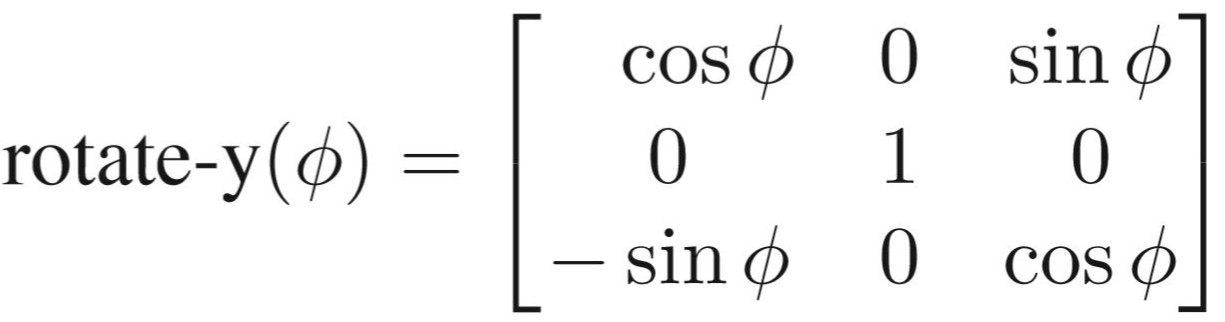
绕任意轴旋转
与2D绕点旋转类似,先把该轴旋转到x或者y或者z轴上,接着就可以应用上面的标准旋转矩阵,最后再把该轴逆旋转回它原先的地方就完成了。用矩阵表示如下:
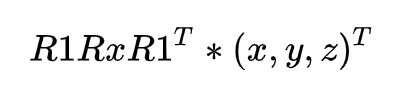
这里的Rx是知道的,也就是3维下绕x轴旋转的矩阵,那么根据之前的分析问题只剩怎么求R1了,设我们想围绕旋转的轴为u,R1便是将u旋转到x的矩阵。 具体来说这里需要以u为一轴,构造一个3维正交坐标系,然后将u和x对齐,那么其它两轴就肯定和y和z对齐了。
构造如下,任取一t方向不与u重合。
w = t x u
v = u x w
此时u, w, v便是我们构造出的新坐标系(这里运用了一些叉乘的几何性质)。
现在得到了u,w,v 对应 x,y,z,如何将这个新坐标系与原始坐标系重合呢?
这其实很简单,直接取R1 = (u,w,v), 该旋转矩阵的含义便是将x, y, z旋转到u,w,v的旋转矩阵(直接计算R1 * x,R1 * y,R1 * z试试便一目了然)。
上一节总结到,旋转矩阵是正交矩阵,旋转矩阵的转置便是它的逆,也是几何意义上的反方向旋转,因此R1T便是将u,w,v旋转到x,y,z的矩阵了。
现在围绕任意轴的旋转矩阵也就得到了。
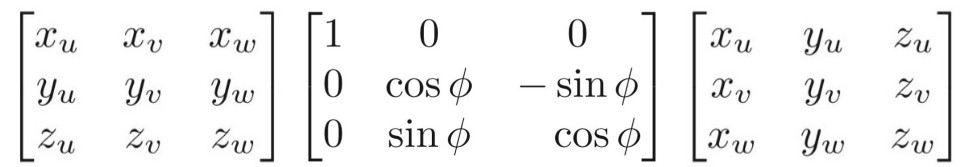
3D齐次坐标
3D的齐次坐标与2D一致,这里不再进行说明,只给出3D线性变换的齐次坐标定义。
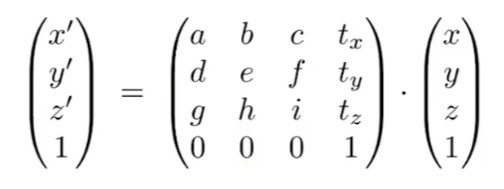
本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》以及孙小磊的计算机图形学系列笔记,感谢。
使卵石臻于完美的,
并非锤的打击,
而是水的且歌且舞。
《飞鸟集》
——泰戈尔






评论
还没有任何评论,你来说两句吧!