前言

在之前的文章《渲染管线基础》中有介绍到在GPU渲染管线里的顶点着色器（Vertex Shader）部分，GPU会将CPU发送过来的模型顶点坐标通过MVP变换矩阵从模型空间（Object Space）转换为裁剪空间（Clip Space），从而完成三维模型向二维屏幕投影的转换过程。

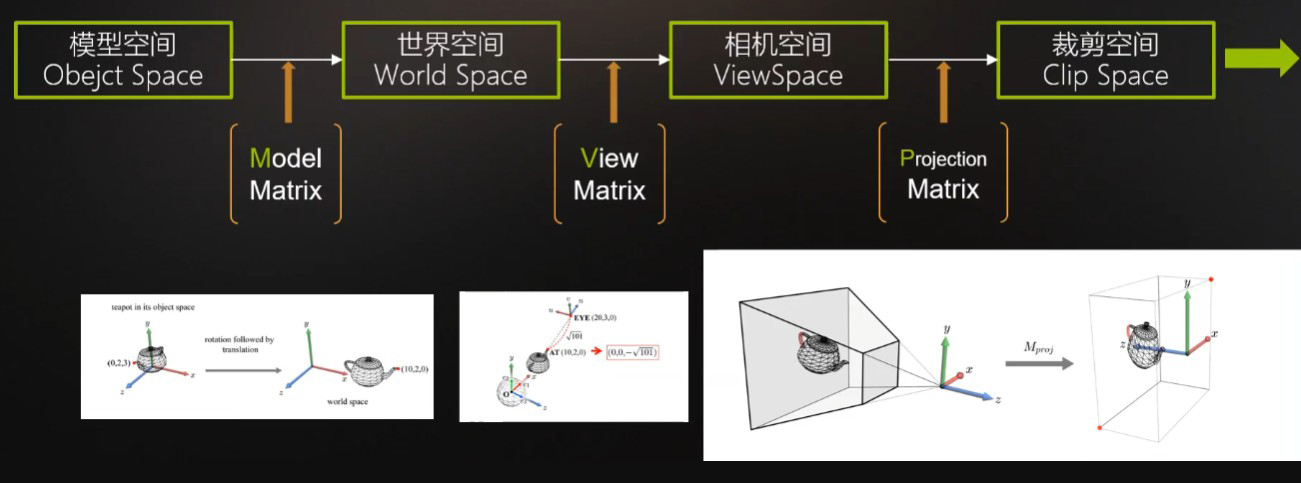
本文就从数学算法来深入介绍这一阶段的具体实现方式。

 

模型变换(modeling tranformation)

这一阶段是将场景中的物体的坐标由模型空间（Object Space）转换到世界空间（World Space），类比于照相时布置拍照的场景。

模型空间是以模型的中心（也可以自定义为其他点，比如重心、初始点等）作为空间坐标系的原点，建立基准坐标系的空间。
每个模型都有自己独立的坐标空间，当它移动或旋转的时候，模型空间也会跟着它移动和旋转。

世界空间的原点以及坐标轴是确定的，使用基础的变换矩阵将场景中的物体调整至对应的位置即可。

 

视图变换(view tranformation)

因为观察视角一般是基于摄像机的，因此视角变换也被称为摄像机变换(camera tranformation)。

这一阶段是将场景中的物体的坐标由世界空间（World Space）转换到观察空间（view Space），摄像机的位置为坐标原点，计算物体此时的相对位置，类比于照相时选择相机的角度。

由于摄像机的位置和角度是不固定的，因此首先要获取当前摄像机的位置（Position），以及摄像机的朝向（Look-at或者Gaze Direction ），还有摄像机向上的方向（Up Direction）。

之后基于摄像机创建观察空间直角坐标系，在这个新的坐标系中，摄像机的坐标为（0, 0, 0），摄像机面对方向为-Z轴（方便后面计算Z-Depth），摄像机向上方向为Y轴，Y轴和Z轴叉乘得到X轴为摄像机右侧方向。

那么对于模型来说，怎么从世界空间转换到这个观察空间呢？

很简单，如果摄像机和场景中所有的东西保持一致进行移动的话，那么整个场景相对于摄像机就是静止的，在摄像机中的画面保持不变。

因此可以将物体和摄像机一起进行移动旋转变换，让摄像机坐标和世界空间坐标原点重合，坐标轴也旋转到观察空间和世界空间一致，这样观察空间和世界空间就是完全重合的，这时物体的世界空间坐标就是它们的观察空间坐标。

对摄像机来说，首先需要从当前位置p平移到世界空间坐标的(0, 0, 0)得到平移变换矩阵，然后当前朝向方向g旋转到世界坐标空间的-Z轴，朝上方向u旋转到Y轴，从而得到旋转变换矩阵。将平移矩阵和旋转矩阵复合出仿射变换矩阵后，再给所有模型的坐标进行应用即可。

第一步平移，只需要减去当前摄像机位置e的坐标即可。

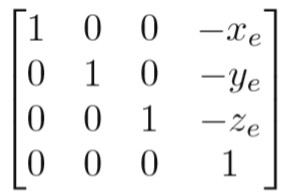
第二步旋转，直接计算这个旋转矩阵比较麻烦，可以反向思考，先写出由世界坐标空间旋转到观察空间的旋转矩阵，然后根据旋转矩阵的逆矩阵就是反向旋转，并且它的逆矩阵等于转置矩阵的原理，转置后就是所需要的旋转矩阵。

即由摄像机朝向g到-Z，摄像机朝上t到Y，g x t到X，就等于Z到-g，Y到t，X到g x t的转置。

 

投影变换(projection tranformation)

投影变换用于在视图变换之后，根据相机设置选择正交投影或是透视投影，将三维空间投影至标准二维平面之上（虽然叫做二维平面，但这里的z坐标并没有丢掉，用于之后的遮挡关系检测）。

这一阶段将物体的坐标从观察空间转换到裁剪空间，类比于照相时按下快门对焦时，不同焦距镜头的视角范围和透视效果不同。

 

正交投影变换(Orthographic Projection Transformation)

正交投影是相对简单的一种，完全没有近大远小的透视效果，坐标的相对位置都不会改变，所有光线都是平行传播，我们只需将物体的xyz坐标全部转换到一个值域[-1, 1]的空间之中即可。

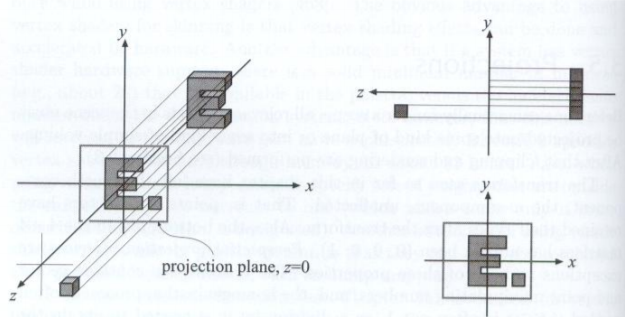
最简单的理解方式就是将所有三维空间的物体挤压到一个二维的平面，也就是将所有物体的z坐标直接去掉，也就实现了从三维到二维平面的映射。

不过实际上z坐标不会被去掉，保留z是为了之后的遮挡检测。

之所以将坐标值域压缩到一个小立方体范围内，是为了之后的计算更加方便，在转换到屏幕坐标的时候会重新拉伸回原来的比例，不必纠结。

这种挤压方式虽然好理解，但为了实现方便，实际一般采用下面这种立方体映射的方法。

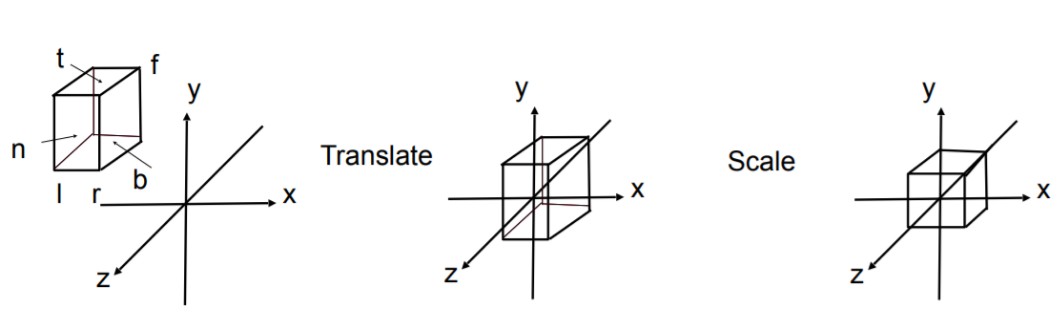
类似模型的Bounding-Box包围盒一样，在X轴上，定义左和右（l和r），在Y轴上，定义下和上（b和t），在Z轴上，定义远和近（f和n）。通过这六个值，就可以定义一个长方体包裹住整个场景。

如何将这么一个范围转换为[-1,1]的空间呢，先通过一个位移矩阵将长方体中心移动到原点，再通过一个缩放矩阵将长方体压缩成一个立方体。

 

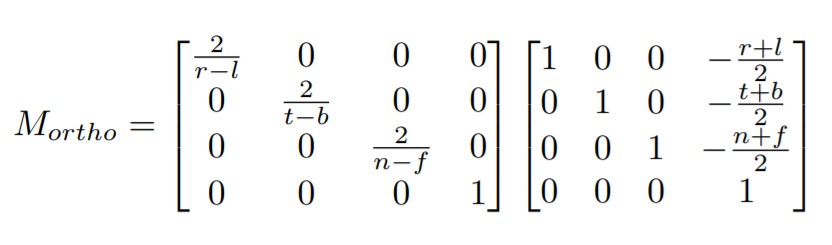
透视投影变换(Perspective Projection Transformation)

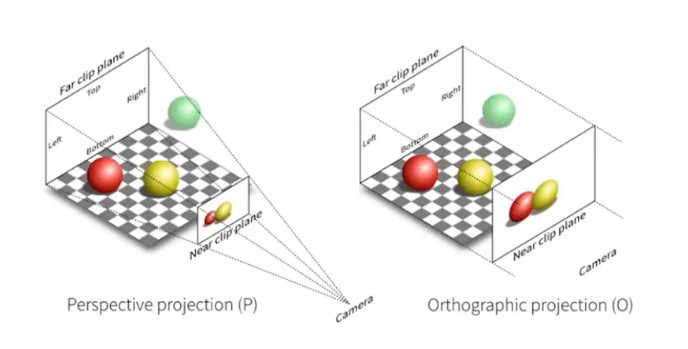
透视投影就是最类似人眼所看东西的方式，遵循近大远小，如果说正交投影都是平行光线，那么透视投影中的平行光线则不再平行，例如上图中平行的铁轨在视线远处相交于一点。

对于透视投影来说，正交投影中的长方体映射不再适用，由于近大远小的透视效果，场景应该包裹在一个有远近截面的四棱锥体中，如下图左所示（摄像机在左侧）。

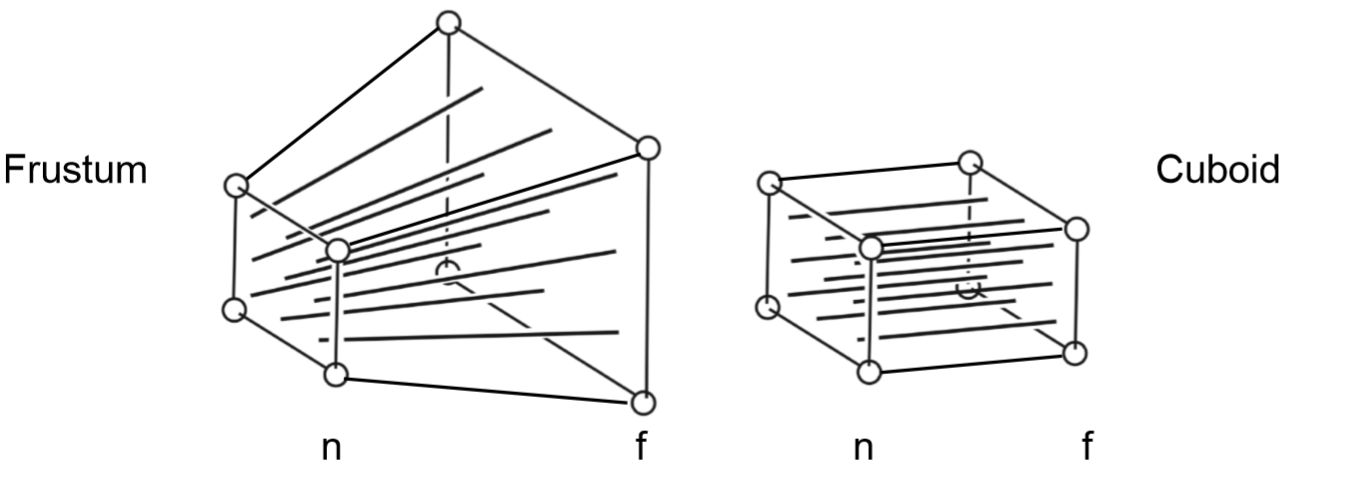
摄像机的可视角度（FOV——field-of-view）以及宽高比（aspect ratio）决定了这个锥体的角度，以及最终投影到屏幕上的宽高比。

为了方便实现，可以先将这个锥体挤压成长方体，再当做正交投影将长方体映射到[-1,1]范围内。

简单理解就是拉住远截面进行挤压缩放，直到远近平面大小相等。

此时，投影过程可用下图解释，将[x,y,z]一点缩放之后，如下所示

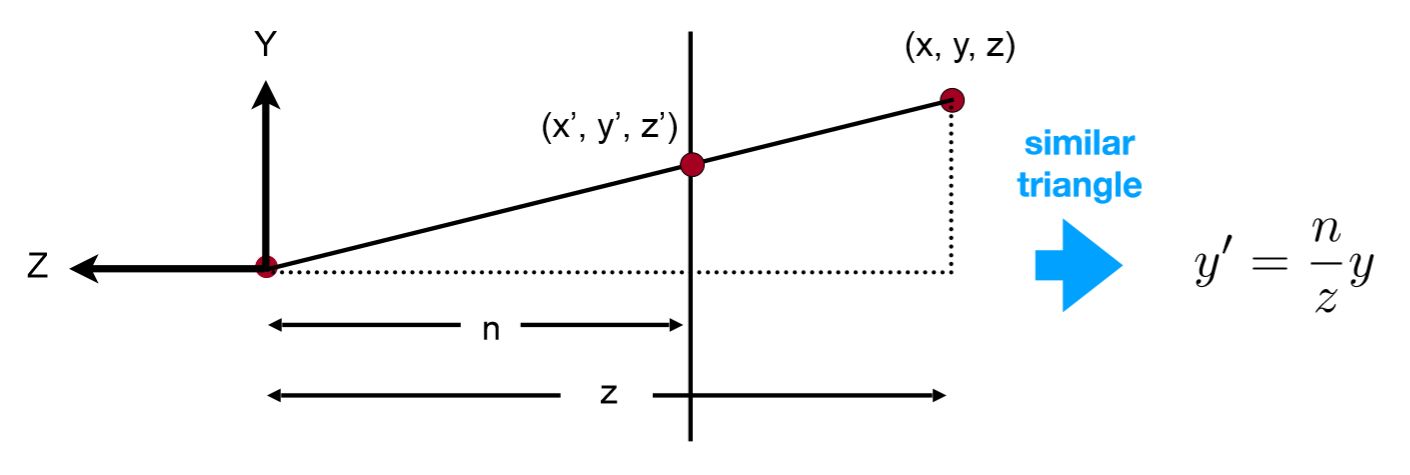
图中原点代表视点，利用相似三角形性质，不难得出图中变换之后的坐标。

齐次坐标有一个性质，就是(x,y,z,1)、(kx,ky,kz,k!=0)、(xz,yz,zz,z!=0)代表了同一个三维空间中的点(x,y,z)。

那么利用齐次坐标的性质，希望找到一个矩阵完成如下变换：

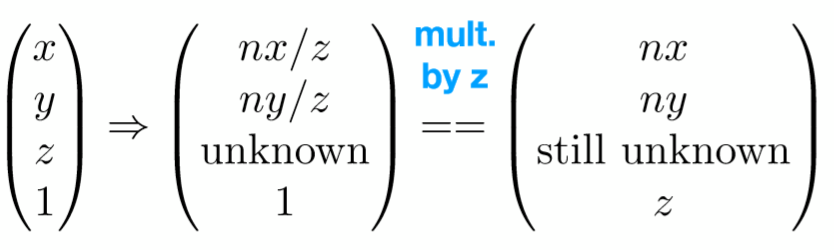
即：

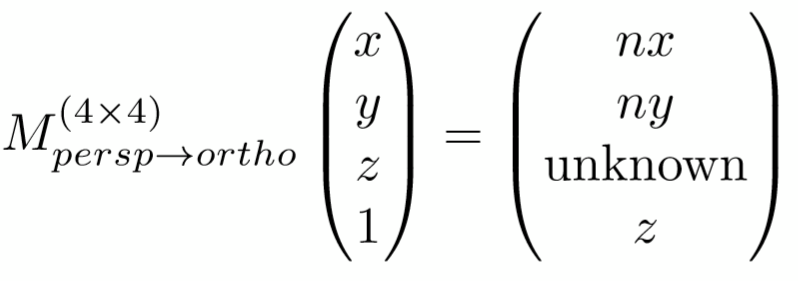
首先，这个矩阵的前两行和最后一行是能很快确定出来的，根据最后的齐次坐标，如下：

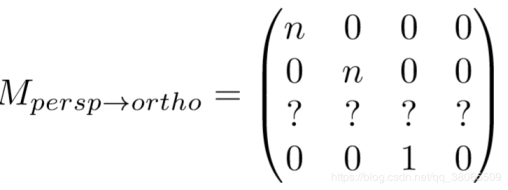
那么如何确定第三行呢，这里就要运用透视投影的两个性质：

• 近截面n上的点变换之后xyz坐标不变。
• 远截面f上的点变换之后z坐标不变，并且中心点x、y坐标也不变。

首先取近平面上任意一点，由于近平面在挤压之后，任何一个点都不会变，所以此时z就可以用n来替代，得到以下式子：

因此第三行的第一第二列必然为零。

我们再选取远平面的中心点，由于远平面的中心点在挤压之后也不会发生变化，x、y依然是0，z=f，所以同理可以写出矩阵：

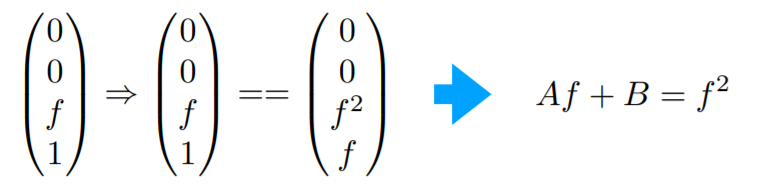
得最后变换矩阵为

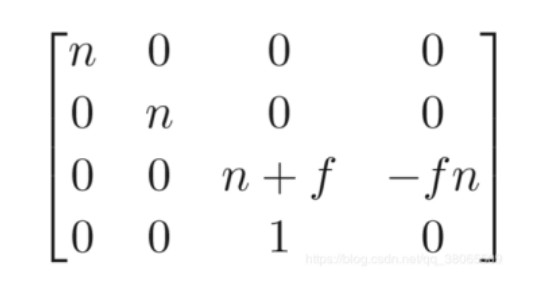
最后的一步，将这个被压缩过的空间，重新正交投影成标准小立方体，故定义透视投影变换Mper如下

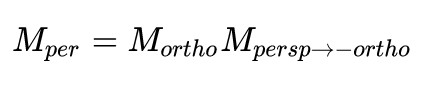
其中两个矩阵都已在上文定义过。计算结果如下：

最后要说的一点是，既然远截面和近截面的点挤压后z坐标不变，那么中间部分的点的z坐标会变化吗？

这里简单给出结论，挤压后点会变远，z坐标会变小，可自行代入得到函数求导证明。

 

视口变换(viewport transformation)

讲完MVP变换矩阵后，最后再说一下在光栅化阶段的屏幕坐标映射（Screen Mapping）步骤如何通过视口变换将这个值域[-1, 1]的立方体缩放回原来的比例投影到屏幕上。

视口变换就是逆向的视图变换，同样是两个立方体范围空间的转换（Z轴不进行变换）。

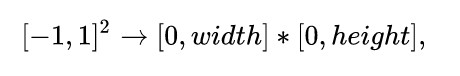
变换矩阵如下

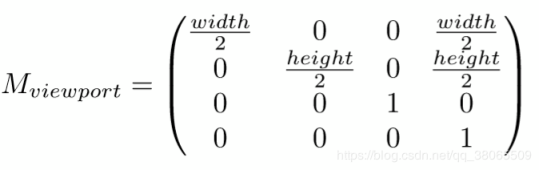
经过上述4个变换，就已经成功的把三维世界的任意可视物体转换到屏幕上了。

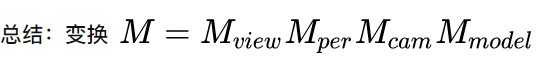
为了与视口变换区分，视图变换此处称作摄像机变换，总的变换矩阵分为M（model模型变换）C（cam视图变换）P（projection投影变换 ）V（view视口变换）四个步骤。

视口变换之前往往还有裁剪、剔除等步骤，因此往往把前三个步骤总称为MVP变换矩阵，视口变换则单列出来。

 

本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》以及孙晓磊的计算机图形学系列笔记，感谢。

---

一束光照进铁塔，
铁塔里的肮脏龌龊被显现，
这束光便有了罪。

——佚名