前言

前面两篇文章说了着色模型以及着色频率，但如果只是给材质一个固定的颜色，最终的效果会很单调，因此需要通过纹理映射让三维物体上的任意一个点都能映射到一个二维贴图上，从而让每一个点得到不同的颜色和属性。

本文就介绍一下这个纹理映射的详细过程以及其中出现的问题。

 

纹理映射

所谓纹理映射，就是三维物体上的任意一个点都映射到一个二维平面，听起来很抽象，其实可以联想一下地球和地图。

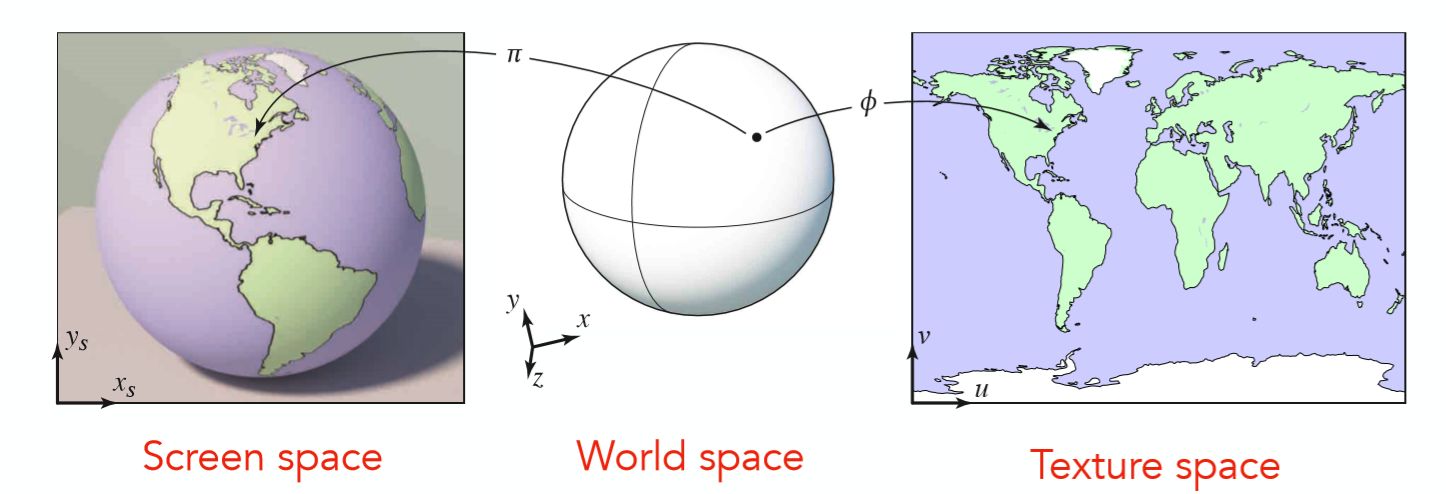
经纬坐标就是地球与地图之间从三维到二维的映射关系，通过经度和纬度两个坐标就可以定义地球表面上一个确切的地点，而对于三维场景中的模型来说，与二维贴图之间的映射关系叫做纹理坐标，也就是UV。如下图就是一个可视化的纹理坐标的结果。

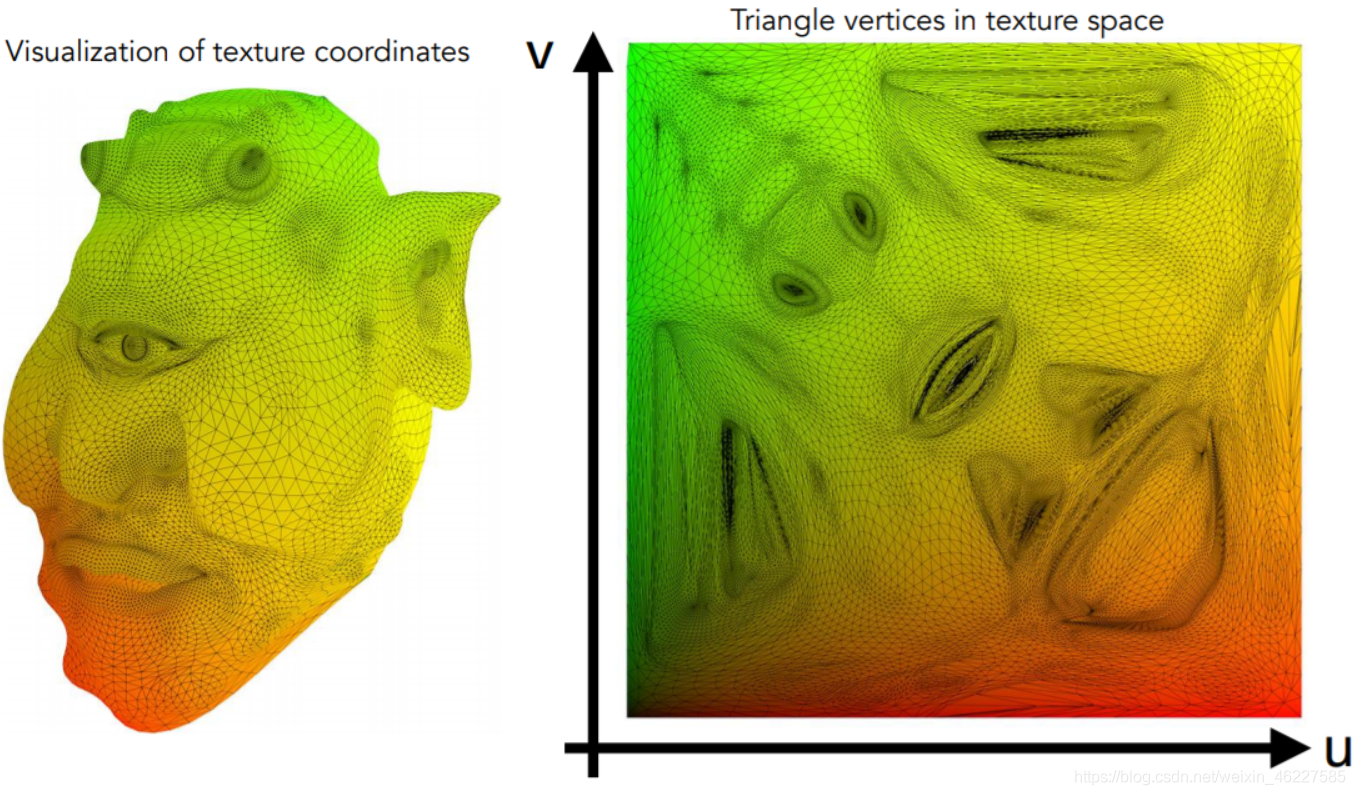
换成绘制好的颜色贴图就是下面这个效果。

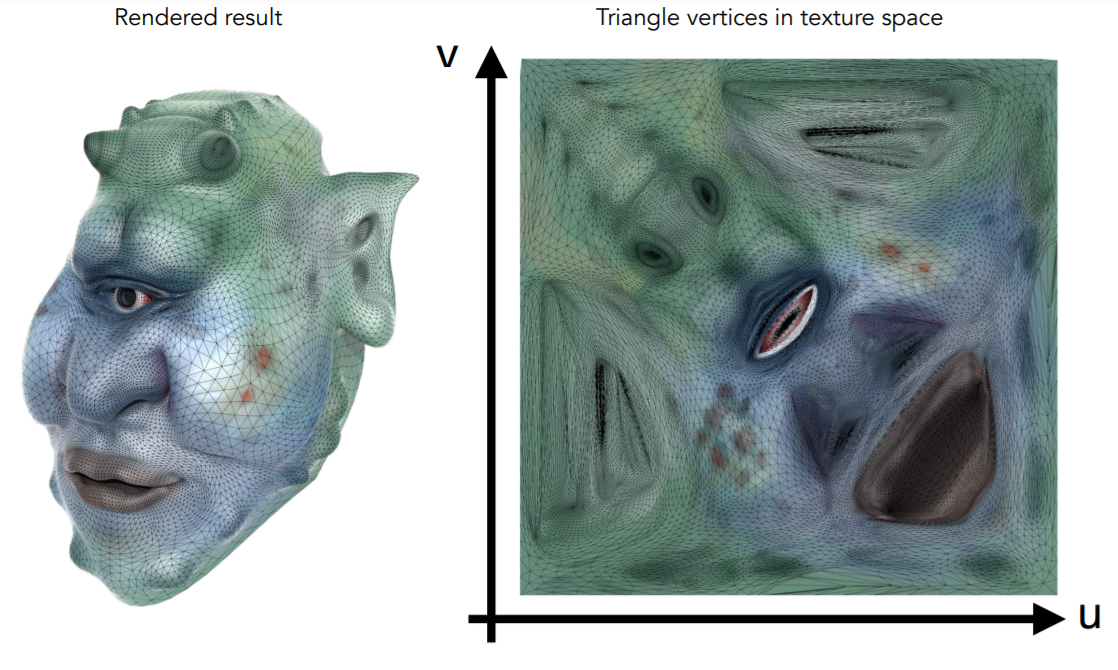
通过u、v这两个坐标，就可以表示纹理上的任意一点，一般u和v的范围都为[0, 1]，显然二维贴图上的点与UV坐标是线性对应关系，那么三维模型的UV坐标又怎么定位呢?

这就需要美术人员在做好模型后进行一个叫做分UV的工作步骤，可以理解为将模型切开展平，尽量平整、少做拉伸地平铺在[0, 1]的UV坐标空间之内。

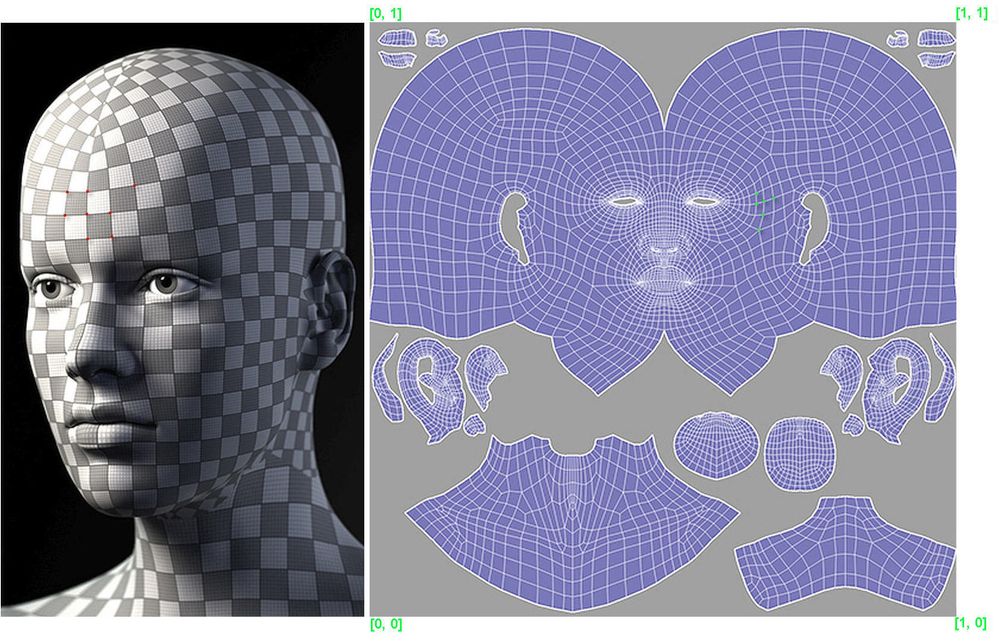
这样三维模型的每个顶点都有自己的uv坐标，存储在模型信息中，而对于三角形内的任意像素点，则可以通过前文说的重心坐标方式求出插值后的UV坐标，从而通过纹理贴图控制模型特定位置的颜色和属性。

 

Tile贴图

对于一些建筑平面例如墙面、地板等等，面积往往较多，并且有一定规律性，此时可以将纹理进行重复拼接使用，为了拼接时不留接缝，往往都会处理成无缝贴图，例如下面的场景

 

纹理过小的问题

当纹理贴图太小时，例如把一张100×100的纹理贴图应用在一个1000×1000的屏幕之上，必然会导致出现马赛克或者模糊，因为屏幕空间相近的几个像素点对应在纹理贴图的坐标上都集中在一个像素大小之内。

那么如果仅仅是使用对应(u,v)坐标在纹理空间下最近的那个像素点采样，就会造成这样的走样现象。

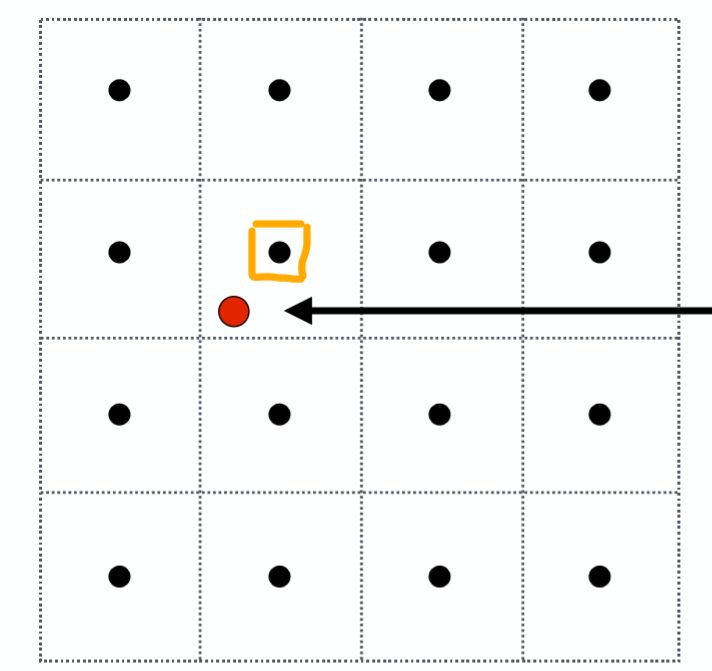
如图中红色点是屏幕空间下一像素所对应在纹理空间中的点，会去采样离他最近的那个纹理颜色点，这种近似采样方法是不可取的。

 

双线性插值(Bilinear Interpolation)

为了避免上面这样的走样现象，于是出现了双线性插值技术。

首先取出离红色点最近的4个黑色顶点，分别算出，该红色点在水平及竖直方向偏移的比率s,t，如下图所示。

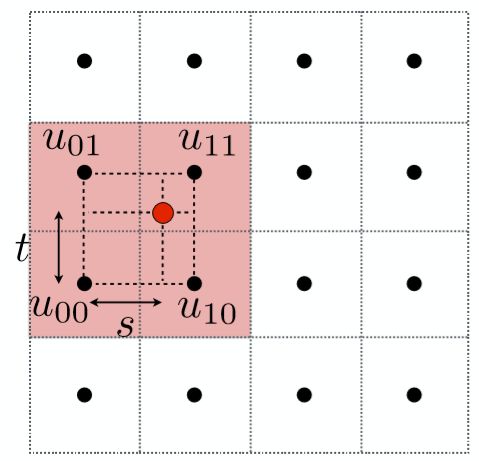
接着利用比例s，线性插值出u00和u10之间u0点的颜色值，以及u01和u11之间的u1点的颜色值

最后利用比例t，对u0和u1线性插值出红色点的颜色值。

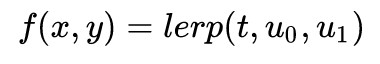
这样利用两次线性插值，考虑到了周围4个点的颜色值，得到了平滑过渡的颜色，能够很好的缓解走样失真现象，并且计算速度较快。

除了双线性插值外，还可以使用双三次插值(Bicubic Interpolation)，取的是周围16个像素而非4个像素（非线性），虽然效果好但是带来的弊端就是开销会很大。

三种插值方式对比效果如下

 

纹理过大的问题

纹理过大直觉上似乎不会有什么问题，但其实在计算机图形学中，反而会导致出现更大的走样问题。

例如有一张很大的地板，在上面铺满了重复的方格贴图，我们所期望看到的结果应该是这样的：

但实际得到的结果往往是这样的

近处有锯齿，远处有摩尔纹，非常严重的走样现象，原因可以参考下图

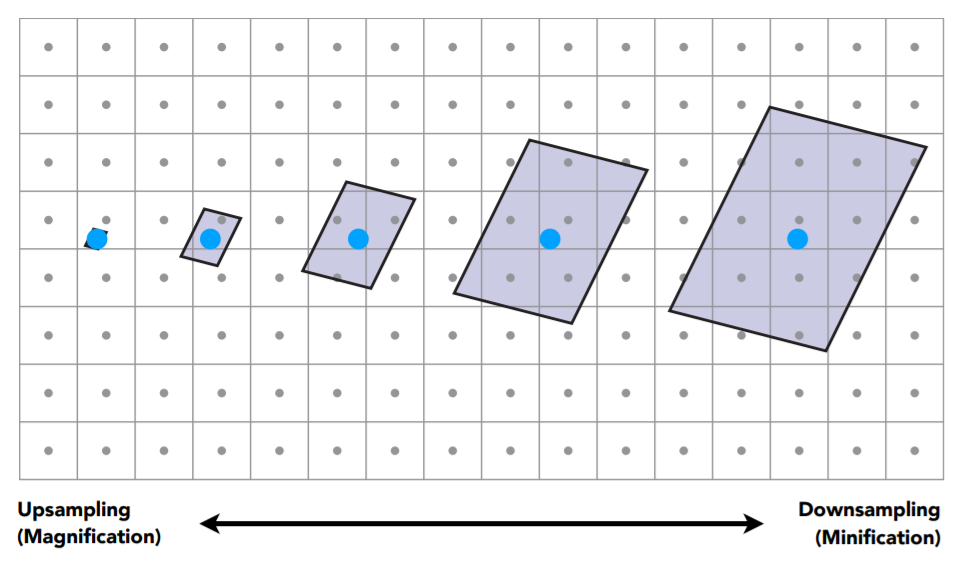
这种屏幕像素对纹理贴图的覆盖区域，被形象的称为屏幕像素在纹理空间的footprint。

显然，由于近大远小的透视关系，对于一个像素来说，近处覆盖的纹理区域相对较小，许多个采样点对应了同一个纹理颜色；而远处覆盖的纹理区域则很大，用一个点的采样无法代表一大块纹理区域的颜色变化。

对于前者，上面说过可以采用双线性插值方法修复，那么后者呢？

暴力一点的话可以采用超采样方式，增加采样点，例如几百倍的超采样，显然可以解决问题，但是付出的代价是极为高昂的计算成本，显然不可取。

那有没有更为便宜的算法，那就要靠Mipmap技术了。

Mip的意思是“multum in parvo”，代表以小寓大，其实就是从一张纹理贴图生成一系列不同大小的贴图。

Level0为原始贴图，每升高一级，分辨率减半，像素数量降到四分之一。

如果原图存储开销是1，因为每一层图分辨率都缩小一半，所以每一层的存储量都是上一层的四分之一，总存储量开销是4/3，额外开销仅仅是1/3。

显然Level每提升一级，4个相邻像素点会求均值合为一个像素点，因此越高的level中一个像素点就能代表更大区域的颜色信息，因此只要让远处的像素找到对应Level的纹理贴图进行采样，就可以解决摩尔纹问题。

那么如何去确定使用哪个level的texture呢？可以利用屏幕像素的相邻像素点映射到纹理上估算footprint大小再确定level 级别D。如下图:

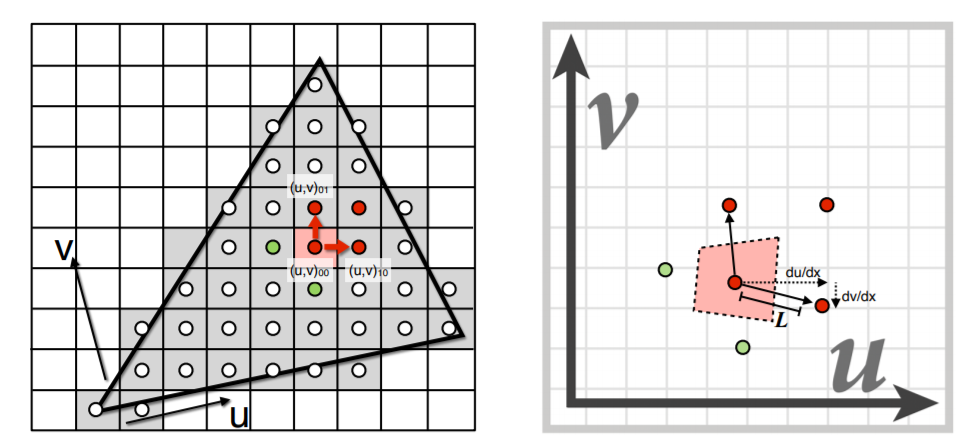
相邻两个像素中心的距离是1，那么对应到右边纹理上占有多远的距离L也就可以求出，这时我们就可以求出一个像素映射到纹理上占据多大的面积。

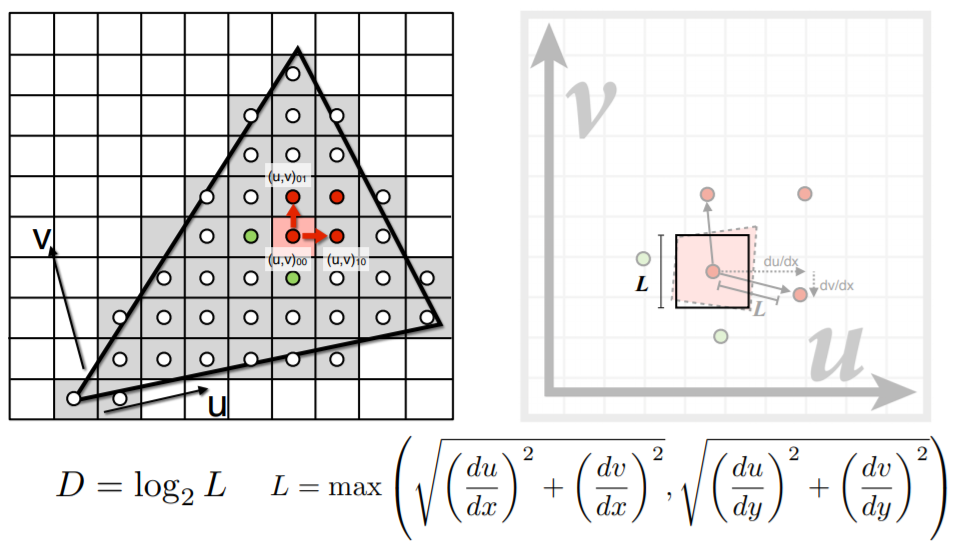
可以用如上图所示的一个正方形框来近似这样一个不规则的区域。

如果这个正方形区域就是1×1，那么就表明一个像素正好对应一个边长为L的正方形区域，也就可以直接在最原始（第0层，D=0）的纹理上找对应的像素，就是它的值。

如歌这个正方形区域是2×2，那么这个区域会在第1层（D=1）上对应一个像素

如果这个正方形区域是4×4，那么这个区域会在第2层（D=2）上对应一个像素

对于L×L大小的正方形，一定会在D=log2L层上对应到一个像素。

因此我们只需要算出D，即在第几层正方形的区域对应一个像素，就可以得需要使用哪一级别的Mipmap。

将这个分层级的结果可视化，如下图所示

可以发现，两层之间有很明显的边界，那么在实际纹理映射的过程中可能会出现一些不明显的缝隙。

 

三线性插值(Trilinear Interpolation)

所谓三线性插值，就是在向下取整的D level上进行一次双线性插值，再在D+1 level上进行一次双线性插值，这二者数据再根据实际的浮点数D值在向下和向上取整的两个不同level之间的比例，再来一次线性插值，而这整体就是一个三线性插值了。

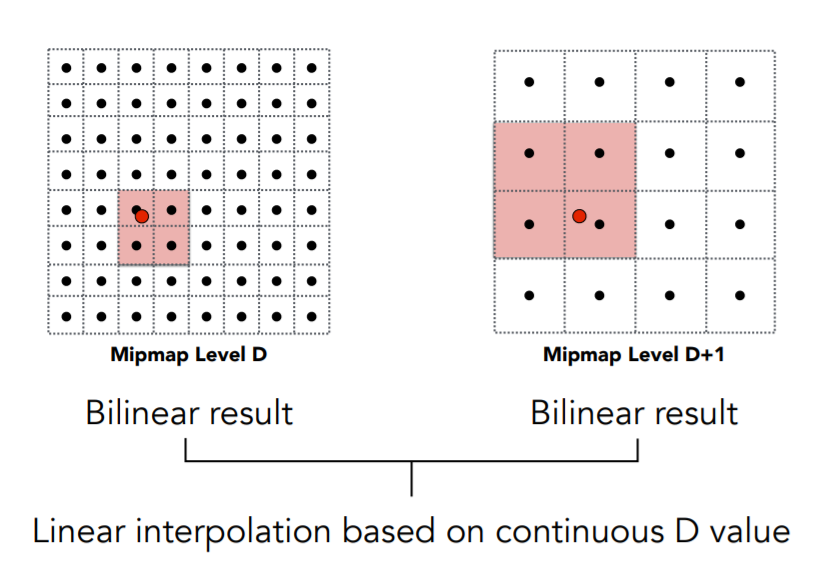
可视化Level效果如下

结果是很漂亮的连续渐变的层级，但遗憾的是，在地板的案例之中，依然不能完美解决走样问题，如下图结果:

虽然和一开始的点采样方式相比有了很大的进步，但有一个严重的问题是，远处的地板产生一种过曝的现象，完全糊在了一起。该如何解决这个最后的问题呢——各向异性过滤。

 

各向异性过滤Mipmap（Ripmap）

产生上面这种现象的原因是因为，所采用的不同level的Mipmap默认的都是正方形区域的采样，然而真实情况并不是如此，见下图:

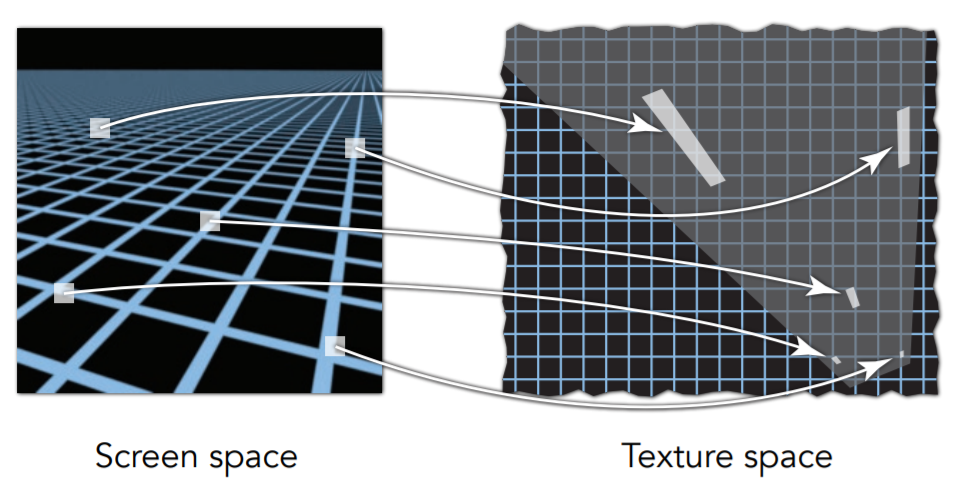
可以看出不同屏幕空间的像素点所对应的footprint是不同的，有长方形，甚至是不规则图形，那么针对这种情况，有的需要水平方向的高level，有的需要竖直方向上的高level，因此也就出现了各向异性的Mipmap：

各向异性可以用不同的长宽比进行缩小，也就是可以用矩形区域做范围查询，而代价就是消耗更多的存储。

利用这样不同比例的Mipmap贴图，结果就会明显好很多:

可以看出，远处过曝的现象已经大大减少了。

但各向异性过滤并不能解决斜着的(diagonal)的footprint，因为各向异性只能解决水平或竖直的不同大小的矩形footprint，所以针对diagonal的footprint，一般是去采样更多的点，或者提前算好diagonal过滤的贴图。

或者通过EWA filtering，对于任何一个形状，都可以拆成很多不同的圆形去覆盖这个形状。

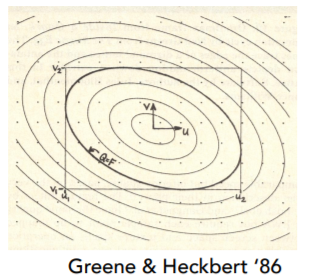
如上图查询一个椭圆，将其拆成三个圆形，每次去查询一个圆形，多次查询自然就可以得到一个区域，但是代价是“多次查询”。可见质量越高的效果，性能开销也就越大。

 

本文参考自本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》和孙晓磊的计算机图形学系列笔记，感谢。

生活的最佳状态是冷冷清清地风风火火。

——木心