前言

前面几篇中说到的光栅化技术是一种速度很快但近似、有偏差的渲染方法，但实际使用中存在难以处理的问题，光栅化技术只能处理直接光照，不能很好地去表示软阴影（Soft Shadow）、光泽反射（Glossy Reflection）和间接照明（Indirect Illumination）等全局光照效果。

而随着计算机硬件性能的提升，出现了光线追踪技术（Ray-Tracing），这种技术能较好地处理全局光照，提高渲染质量，但目前还不能完全替代光栅化技术。因为光线追踪技术的计算非常慢，在诞生以来更多被用来做离线渲染，比如三维动画、电影特效等等，因为只需要计算一次输出成图片给观众观看即可。

而游戏是需要实时计算的，因此直到近几年随着NVIDIA的RTX系列显卡的不断迭代，硬件光线追踪技术和游戏引擎功能的进步，现在的3A级游戏大作才慢慢支持了实时光线追踪技术（Real-Time Ray-Tracing）。

只不过当前所谓的光线追踪技术已经成了一个大的门类，包含了传统的Whitted-style光线追踪、路径追踪（Path Tracing）、光子映射（Photon Mapping）、Metropolis光线传输（Metropolis light transport ）等各种用于计算全局光照的技术。

今天就先来介绍一下最经典的Whitted-style光线追踪算法。

光线追踪的原理

没错这就是光线追踪的核心想法，以摄像机为起点通过虚拟屏幕中的每个像素发射一条光线，追踪每条光线在场景中的反射折射，查询光线与物体的交点，计算得到每个像素最终的颜色！

之所以不采用正向模拟光线，是因为光源发射出的绝大多数光线都不会直接进入摄像机，正向模拟会在无效的光路上浪费大量计算，因此逆向模拟的效率要高出很多个数量级。

这种光线追踪算法与自然界的光线传播方向是相反的，因此有人称之为逆向光线追踪，但因为传统的光线追踪算法都是摄像机发射光线，后来则出现了从光源发射光线的逆向光线追踪算法，甚至于同时采用摄像机发射光线和光源发射光线的双向路径追踪，因此为避免混淆，一般称为基于眼睛（ eye-based）的光线追踪和基于光源（ light-based）的光线追踪。

Whitted-style光线追踪的步骤

Whitted-style光线追踪算法是由Turner Whitted在1980年提出的，用于解决复杂曲面的反射折射效果，主要有以下两个步骤：

Ray Casting

首先做几个假设：

1、眼睛是针孔摄像机，假设为一个点

2、光源假设是点光源

3、反射折射是完美的（镜面反射）

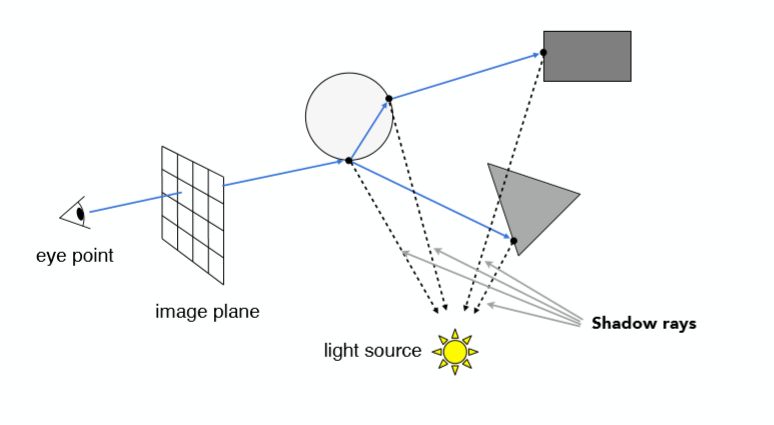
从人眼或摄像机向近投影平面上的每一个像素点发射一条光线，称为Eye Ray，判断与场景物体的交点，示意图如下：

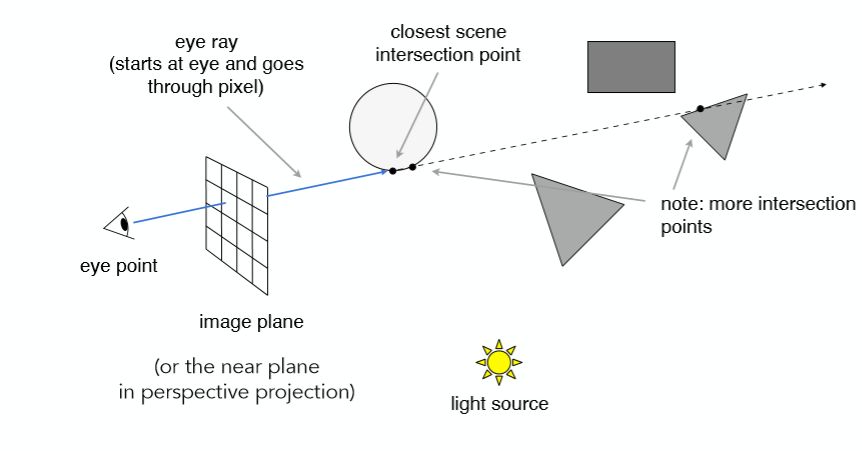
当然一条光线可能会与不止一个物体相交，但是考虑遮挡关系，只去找最近的交点（方便地解决遮挡问题，光栅化中则是通过深度缓存z-buffer解决遮挡问题），说明从摄像机中能够看到这个物体与光线的交点。

接着连接该交点和光源（Shadow Rays），判断这个点是不是对光源也可见，如果这条连线之间有物体存在就可以知道该交点在阴影之中（相比于光栅化的shadow mapping，光线追踪技术在着色时就可以计算阴影）：

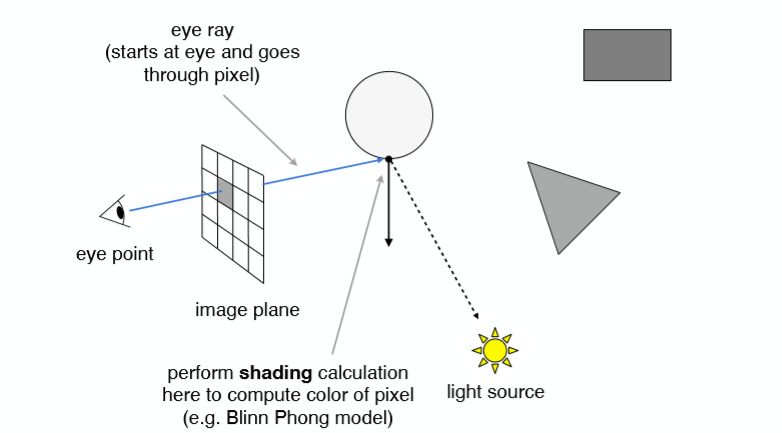
但如果光线追踪仅仅是在第一步Ray Casting就停止的话，那么它的效果与局部光照模型是类似的，因此我们需要第二步，真正的考虑全局效果。

Recursive Ray Tracing（递归光线追踪）

当光线与物体相交时，如果该交点处是不透明的漫反射材质，那么就可以像前面所说在第一步Ray Casting就停止。

而如果该交点处是不透明的光滑镜面材质，那么光线便会发生反射并损失少量能量，继续沿光路传递寻找下一个碰撞物体，如图：

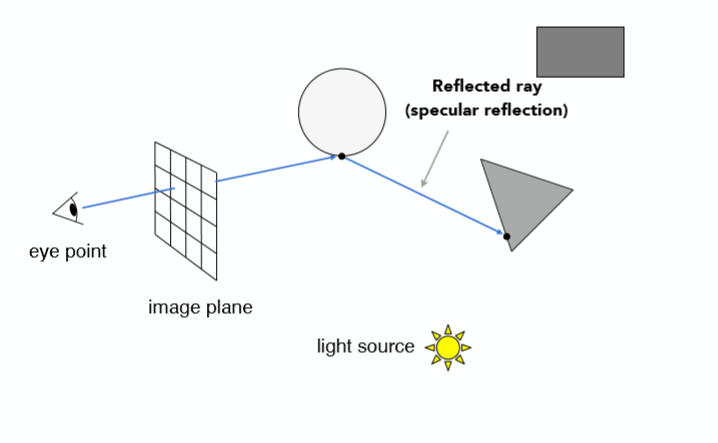
而如果该交点处是透明的玻璃材质，那么除了反射之外，玻璃球内部也会发生光线的折射，反射光和折射光都会沿光路继续向前走，能量都有损失。

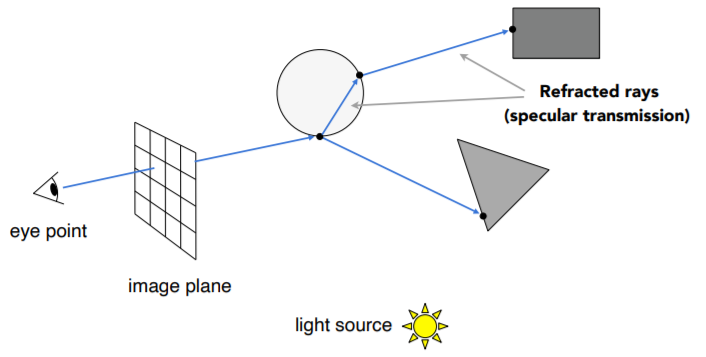
同时反射与折射出去的光线可能会与场景中的物体再次碰撞，发生第二次反射和折射等：

递归光线追踪就体现在反射和折射光线上，当场景中有大量光滑镜面材质物体和透明材质物体时，光线会不断进行反射和折射，导致计算量失控，因此需要一定的递归终止条件，比如说允许的最大反射或折射次数为10。

因此每一个像素点的颜色来自这样几种类型的光照：直接光照、间接反射光照，间接折射光照（如果有折射的话），下一步将这些光路上的所有交点与光源连接，称这些线为Shadow Rays（因为可以用来检测阴影），计算这些所有交点的局部光照模型的结果，将其按照光线能量权重累加，最终得到近投影平面上该像素点的颜色！

之所以用光线能量权重，是因为光线在每次反射和折射之后都有能量损耗的，因此递归层级越多的折射和反射光贡献的能量越小， 例如反射权重系数为0.7，那么第一次反射折损30%，第二次反射折损1-(70%x70%)，依次类推。

另外如果反射或折射光线没有碰撞到物体，一般会终止该光线并返回一个背景色。

而这就是一个考虑全局效果的光照模型了，因为不仅仅考虑了直接光源的贡献，还考虑各种反射与折射光线的贡献，最终得到的效果如下。

在四十多年前能够得到这样逼近照片级的效果，可以看出该算法的强大，而随着硬件性能的提升，当年这个需要几十分钟才能渲染出的场景，如今的硬件已经可以做到每秒几千帧了。

光线追踪与光栅化的区别

光栅化的过程是枚举每个像素的位置，从摄像机向像素连线，找到碰到的第一个物体的交点（通过 z-buffer深度缓存 解决遮挡问题），然后根据光源计算颜色（例如 Blinn-Phong 等反射模型），根据光源的z-buffer深度缓存计算阴影（shadow mapping技术）。

换句话说，就是摄像机 – 物体 – 光源，光线只发射了一次，也就是只考虑了直接光照。

而光线追踪则是枚举每个像素的位置，从摄像机向像素连线，找到碰到的第一个物体的交点（通过光线与平面的交点算法 解决遮挡问题），根据光源计算颜色（例如 Blinn-Phong 等反射模型，并通过交点与光源连线是否被遮挡来计算阴影），然后计算反射/折射方向，计算从该点该方向射出的光线碰到的第一个物体的交点，根据光源计算颜色，这样递归计算。最后再计算每个交点叠加起来的总贡献。

换句话说，就是摄像机 – (物体-光源) – (物体-光源) – …，光线是可以多次反射、折射的，也就是考虑到了直接光照和间接光照。

光线与平面的交点算法

光线方程（Ray Equation）

光线是一条射线，数学意义上可以表示为一个原点和一个方向，考虑到光线传播的时间参数，因此一般表示为以下形式。

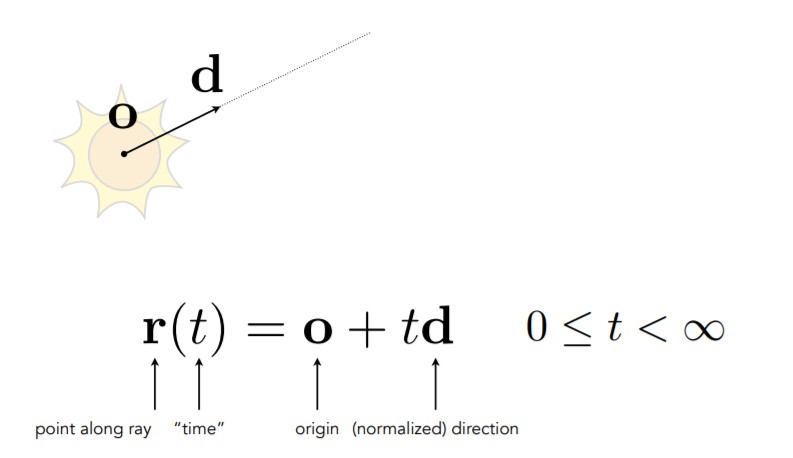
对于光线上任意一点r，在t时间，都可以表示为从起始位置o，加上t乘以向量d。对于t来讲，由于这里是射线，而且t表示时间，所以t不能取负数值。

光线与隐式曲面求交

首先介绍如何计算光线与隐式曲面的交点的方法，以一个球体为例，二者表示方程如下：

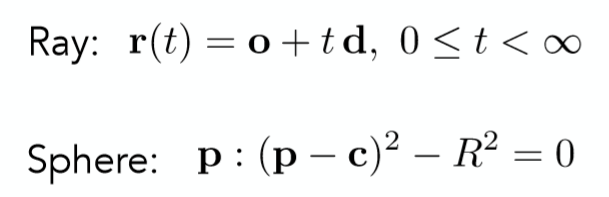
光线的表示方法在上节已经介绍过，对于一个球体来说，其表面上所有点P, 到圆心C的距离是固定为R的， 也就得到了上述的球的隐式曲面方程。

那么对于一个光线会在什么时候与球相交呢？

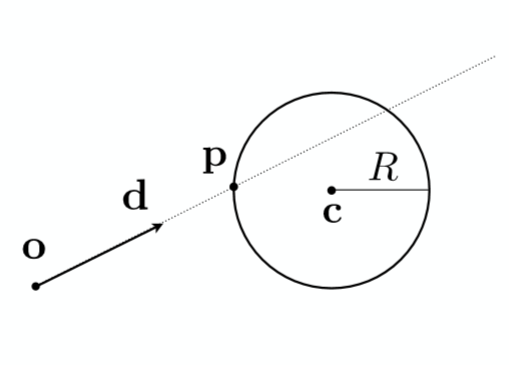
当然是在一个点即满足光线方程，又满足球体方程的时候，所以可以计算如下，把 P=O+td代入球体方程，利用一元二次方程的解法即可得到参数 t 值：

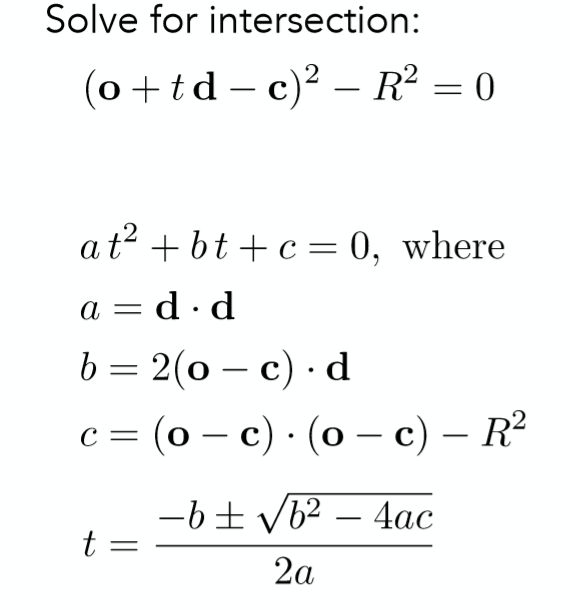
同样的根据 bb-4ac 的正负关系，即可判断光线与球是一个交点还是两个交点又或是没有交点。

虽然这里只举了对一个球的隐式曲面交点的计算，对于所有其他隐式曲面过程都是类似的，只要将光线方程代入求解 t 即可，如下图所示

光线与显式曲面求交

当然，真正在图形学中大量运用的其实是显式曲面，更具体来说就是许许多多个三角形，因此如何判断一条光线与显式曲面的交点，其实也就是计算光线与三角形面的交点。

对于任意一个平面，可以定义成一个法线以及平面上的一个点，也就是立体几何中的点法式，用如下图中的式子表达：

对于任意一个三角面来说，它一定处于一个平面之上，只需求出光线与平面的交点，再判断该交点是否在三角形内，就可以得到光线是否与三角形面相交的结果了！

这样其实已经成功把对显示曲面的求交转化为了类似隐式曲面求交的方式。

首先给出如何计算光线与平面交点的过程：

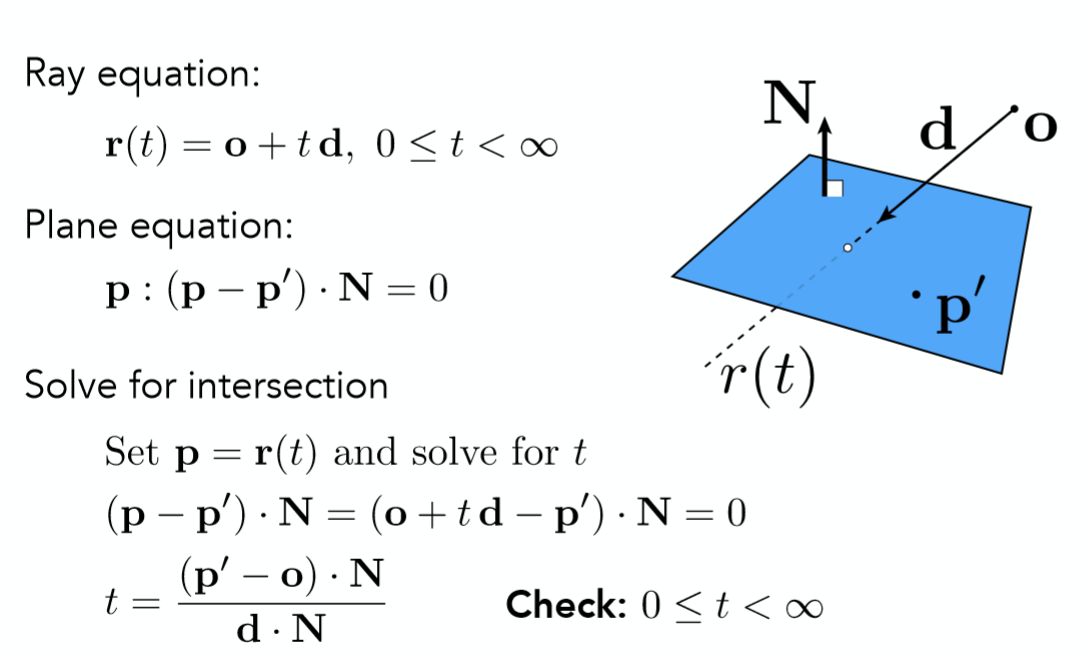
如果要求光线和球的交点，那么说明这个点既要满足光线上一点的定义也要满足平面上一点的定义，联立这两个式子，就可以得到 t。

得到参数 t 之后，自然可以计算出交点，并且再去计算出重心坐标就能判断该交点是否在三角形内了，但是这种方法略显繁琐，能不能一步就得到结果呢？

当然可以！

直接将点的形式用重心坐标的形式表示，随后利用克莱姆法则求解线性方程组即可得到t和b1、b2的值，那么只要该点的重心坐标1-b1-b2、b1、b2都是非负数，那么就说明该点在三角形内。

本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》和孙晓磊的计算机图形学系列笔记，感谢。

每个人心里都有一团火，
但路过的人只能看到烟。

——梵高